
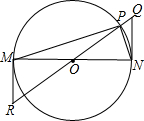
 如图,过圆O直径的两端点M、N各引一条切线,在圆O上取一点P,过O、P两点的直线交两切线于R、Q.
如图,过圆O直径的两端点M、N各引一条切线,在圆O上取一点P,过O、P两点的直线交两切线于R、Q.分析 (1)只要证明两角对应相等即可证明.
(2)作NF⊥RQ于F,MK⊥RQ于K,连接ME,先证明△OMR≌△ONQ,得到OR=OQ,MK=FN,由题意S△PMR=4S△PNQ,推出PR=4PQ,即2$\sqrt{5}$+a=4a,求出a,然后利用勾股定理求出QN、利用面积法求出FN,再利用勾股定理即可解决问题.
解答 (1)证明:∵NQ、RM是⊙O切线,
∴NQ⊥MN,MR⊥MN,
∴NQ∥MR,
∴∠Q=∠R,
∵MN是直径,
∴∠MPN=∠MNQ=90°,
∴∠MNP+∠NMP=90°,∠MNP+∠PNQ=90°,
∴∠QNP=∠NMP,
∵OM=OP,
∴∠OPM=∠OMP,
∴∠QNP=∠RPM,
∴△NPQ∽△PMR.
(2)解:作NF⊥RQ于F,MK⊥RQ于K,连接ME,
在△OMR和△ONQ中,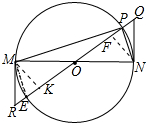
$\left\{\begin{array}{l}{∠R=∠Q}\\{∠RMO=∠QNO}\\{OM=ON}\end{array}\right.$,
∴△OMR≌△ONQ,
∴OR=OQ,MK=FN(全等三角形对应边上高相等)
∵OE=OP,
∴RE=PQ,时PQ=RE=a,
由题意S△PMR=4S△PNQ,
∴PR=4PQ,即2$\sqrt{5}$+a=4a,
∴a=$\frac{2\sqrt{5}}{3}$.
在RT△ONQ中,∵∠ONQ=90°,ON=$\sqrt{5}$,OQ=$\frac{5\sqrt{5}}{3}$,
∴NQ=$\sqrt{O{Q}^{2}-O{N}^{2}}$=$\frac{4\sqrt{5}}{3}$,
∵$\frac{1}{2}$•OQ•FN=$\frac{1}{2}$•ON•QN,
∴FN=$\frac{4\sqrt{5}}{5}$,
在RT△OFN中,∵∠OFN=90°,ON=$\sqrt{5}$,FN=$\frac{4\sqrt{5}}{5}$,
∴OF=$\sqrt{O{N}^{2}-F{N}^{2}}$=$\frac{3\sqrt{5}}{5}$,
在RT△PNF中,∵∠PFN=90°,PF=$\frac{2\sqrt{5}}{5}$,FN=$\frac{4\sqrt{5}}{5}$,
∴PN=$\sqrt{P{F}^{2}+F{N}^{2}}$=2.
点评 本题考查相似三角形的判定和性质、全等三角形的判定和性质、勾股定理,面积法求高等知识,解题的关键是添加辅助线,学会灵活运用勾股定理、面积法,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 某工厂要制作一个容积为300立方厘米的正方体形状的无盖水槽(如图所示).准备用钢板焊制,试求至少要用多少平方厘米的钢板?(结果精确到1平方厘米)
某工厂要制作一个容积为300立方厘米的正方体形状的无盖水槽(如图所示).准备用钢板焊制,试求至少要用多少平方厘米的钢板?(结果精确到1平方厘米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
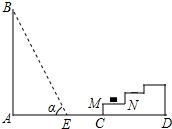 如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.
如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{1}{3}<-\frac{3}{2}<-0.2<-1$ | B. | $-\frac{1}{3}<-0.2<-1<-\frac{3}{2}$ | C. | $-\frac{3}{2}>-1>-\frac{1}{3}>-0.2$ | D. | $-0.2>-\frac{1}{3}>-1>-\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com