
分析 (1)由于已知抛物线与x的两交点坐标,则可设交点式y=a(x+3)(x-1),然后把C(0,3)代入求出a的值即可.
(2)利用配方法求该抛物线的顶点坐标和对称轴.
解答 解:(1)设抛物线解析式为y=a(x+3)(x-1)(a≠0).
把C(0,3)代入得a×3×(-1)=3,
解得a=-1.
故该抛物线解析式为:y=-(x+3)(x-1)或y=-x2-2x+3.
(2)∵y=-x2-2x+3=-(x+1)2+4.
∴抛物线的顶点坐标是(-1,4),对称轴是x=-1.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,?ABCD中,点E、F在直线AC上,BE∥DF.
如图,?ABCD中,点E、F在直线AC上,BE∥DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
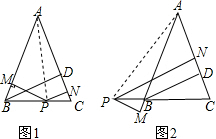 如图1,在△ABC中,AB=AC,BD是△ABC的高,P是BC边上一点,PN分别与直线AB,AC垂直,垂足分别为点M,N,求证:BD=PM+PN.
如图1,在△ABC中,AB=AC,BD是△ABC的高,P是BC边上一点,PN分别与直线AB,AC垂直,垂足分别为点M,N,求证:BD=PM+PN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在热气球上A处测得一栋大楼顶部B的俯角为23°,测得这栋大楼底部C的俯角为45°.已知热气球A处距地面的高度为180m,求这栋大楼的高度(精确到1m).(参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42)
如图,在热气球上A处测得一栋大楼顶部B的俯角为23°,测得这栋大楼底部C的俯角为45°.已知热气球A处距地面的高度为180m,求这栋大楼的高度(精确到1m).(参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
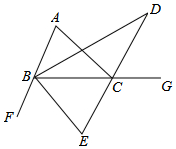 如图,∠CBF、∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC、∠CBF的平分线BD、BE交于点D、E.
如图,∠CBF、∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC、∠CBF的平分线BD、BE交于点D、E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com