
【题目】某校为改善办学条件,计划购进A,B两种规格的书架,经市场调查发现有线下和线上两种购买方式,具体情况如下表:

(1)如果在线下购买A,B两种书架20个,共花费5520元,求A,B两种书架各购买了多少个.
(2)如果在线上购买A,B两种书架20个,共花费W元,设其中A种书架购买m个,求W关于m的函数关系式.
(3)在(2)的条件下,若购买B种书架的数量不少于A种书架数量的2倍,请求出花费最少的购买方案,并计算按照这种购买方案,线上比线下节约多少钱?
【答案】(1)A种书架购买了8个,B种书架购买了12个;(2)W=-50m+5600;(3)当购买6个A种书架,14个B种书架时,花费最少,按照这种购买方案,线上比线下节约340元
【解析】
(1)设购买A种书架x个,则购买B种书架(20﹣x)个,根据买两种书架共花费5520元,列方程求解即可;
(2)W=买A种书架的花费+买B种书架的花费+运费,列式即可;
(3)根据购买B种书架的数量不少于A种书架的2倍,求出m的取值范围,再根据第(2)小题的函数关系式,求出W的最小值即线上的花费,再求出线下需要的花费即可.
解:(1)设购买A种书架x个,则购买B种书架(20-x)个.
根据题意,得
240x+300(20-x)=5520,
解得x=8,
则20-8=12(个).
答:A种书架购买了8个,B种书架购买了12个.
(2)根据题意,得
W=210m+250(20-m)+20m+30(20-m)
=-50m+5600.
(3)根据题意,得
20-m≥2m,解得
m≤![]() .
.
∵-50<0,
∴W随m的增大而减小,
∴当m=6时,W最小,W最小=-50×6+5600=5300,
此时20-m=14.
线下购买时的花费为240×6+300×14=5640(元),5640-5300=340(元).
答:当购买6个A种书架,14个B种书架时,花费最少,按照这种购买方案,线上比线下节约340元.


科目:初中数学 来源: 题型:
【题目】如图,已知平面直角坐标系,![]() 两点的坐标分别为
两点的坐标分别为![]() .
.
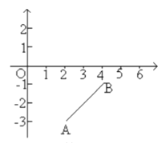
(1)若![]() 是
是![]() 轴上的一个动点,则当
轴上的一个动点,则当![]() _______时,
_______时,![]() 的周长最短;
的周长最短;
(2)若![]() 是
是![]() 轴上的两个动点,则当
轴上的两个动点,则当![]() _______时,四边形
_______时,四边形![]() 的周长最短;
的周长最短;
(3)设![]() 分别为
分别为![]() 轴和
轴和![]() 轴上的动点,请问:是否存在这样的点
轴上的动点,请问:是否存在这样的点![]() , 使四边形
, 使四边形![]() 的周长最短?若存在,请求出,
的周长最短?若存在,请求出,![]() _________,
_________,![]() ________(不必写解答过程);若不存在,请说明理由.
________(不必写解答过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
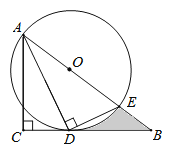
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.
(1)求证:直线BC是⊙O的切线;
(2)若∠ABC=30°,⊙O的直径为4,求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的二次函数
的二次函数![]() (
(![]() >0)的图象经过点C(0,1),且与
>0)的图象经过点C(0,1),且与![]() 轴交于不同的两点A、B,点A的坐标是(1,0).
轴交于不同的两点A、B,点A的坐标是(1,0).
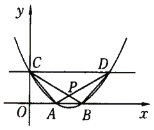
(1)求c的值和![]() ,
,![]() 之间的关系式;
之间的关系式;
(2)求![]() 的取值范围;
的取值范围;
(3)该二次函数的图象与直线![]() 交于C、D两点,设 A、B、C、D四点构成的四边形的对角线相交于点P,记△PCD的面积为S1,△PAB的面积为S2,当0<
交于C、D两点,设 A、B、C、D四点构成的四边形的对角线相交于点P,记△PCD的面积为S1,△PAB的面积为S2,当0<![]() <l时,求证:S1-S2为常数,并求出该常数.
<l时,求证:S1-S2为常数,并求出该常数.
查看答案和解析>>
科目:初中数学 来源: 题型:
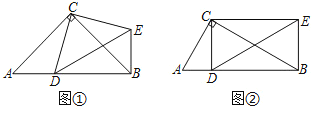
【题目】综合与实践
在Rt△ABC中,∠ACB=90°,点D为斜边AB上的动点(不与点A,B重合).
(1)操作发现:如图①,当AC=BC=8时,把线段CD绕点C逆时针旋转90°得到线段CE,连接DE,BE.
①∠CBE的度数为 ;
②当BE= 时,四边形CDBE为正方形;
(2)探究证明:如图②,当BC=2AC时,把线段CD绕点C逆时针旋转90°后并延长为原来的两倍,记为线段CE,连接DE,BE.
①在点D的运动过程中,请判断∠CBE与∠A的大小关系,并证明;
②当CD⊥AB时,求证:四边形CDBE为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】忽如一夜春风来,千树万树梨花开.在清明假期期间,小梅和小北姐弟二人准备一起去乐陵大孙乡采摘园赏梨花,但因家中临时有事,必须留下一人在家,于是姐弟二人采用游戏的方式来确定谁去赏梨花.游戏规则是:在不透明的口袋中分别放入2个白色和1个黄色的乒乓球,它们除颜色外其余都相同.游戏时先由小梅从口袋中任意摸出1个乒乓球记下颜色后放回并摇匀,再由小北从口袋中摸出1个乒乓球,记下颜色.如果姐弟二人摸到的乒乓球颜色相同,则小梅赢,否则小北赢.则小北赢的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
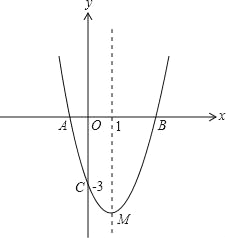
【题目】(11分)如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴交于C点,且经过点(2,﹣3a),对称轴是直线x=1,顶点是M.
(1)求抛物线对应的函数表达式;
(2)经过C,M两点作直线与x轴交于点N,在抛物线上是否存在这样的点P,使以点P,A,C,N为顶点的四边形为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)设直线y=﹣x+3与y轴的交点是D,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,试判断△AEF的形状,并说明理由;
(4)当E是直线y=﹣x+3上任意一点时,(3)中的结论是否成立(请直接写出结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
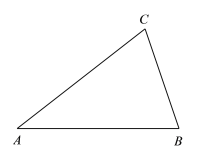
【题目】如图,已知△ABC中,AB=AC.
(1)把△ABC绕点C顺时针旋转得到△DEC,使得点B的对应点E落在AB边上,用尺规作图的方法作出△DEC;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接AD,求证:AD=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
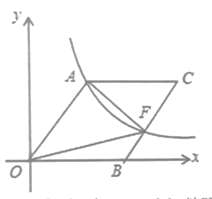
【题目】如图,在直角坐标系中,四边形OACB为菱形,OB在x轴的正半轴上,∠AOB=60°,过点A的反比例函数y= ![]() 的图像与BC交于点F,则△AOF的面积为 ______________.
的图像与BC交于点F,则△AOF的面积为 ______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com