
科目:初中数学 来源: 题型:解答题
 如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,若BD与AC的和为23,AB:AD=1:2,△COD的周长为15,求BC的长.
如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,若BD与AC的和为23,AB:AD=1:2,△COD的周长为15,求BC的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,经过点A的双曲线y=$\frac{k}{x}$(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为$\sqrt{2}$,∠AOB=∠OBA=45°,则k的值为1+$\sqrt{5}$.
如图,在平面直角坐标系中,经过点A的双曲线y=$\frac{k}{x}$(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为$\sqrt{2}$,∠AOB=∠OBA=45°,则k的值为1+$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
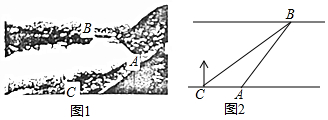 如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走50m到达C点,测得点B在点C的北偏东60°方向,如图2,求出这段河的宽(结果精确到1m,备用数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73).
如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走50m到达C点,测得点B在点C的北偏东60°方向,如图2,求出这段河的宽(结果精确到1m,备用数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的边长AD为⊙O的直径,E是AB上一点,将正方形的一个角沿EC折叠,使得点B恰好与圆上的点F重合,则tan∠AEF=$\frac{3}{4}$.
如图,正方形ABCD的边长AD为⊙O的直径,E是AB上一点,将正方形的一个角沿EC折叠,使得点B恰好与圆上的点F重合,则tan∠AEF=$\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com