
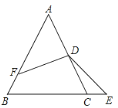
【题目】如图,已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则![]() =____.
=____.
【答案】![]()
【解析】
过D作DG∥BC交AB于G,则DG为△ABC的中位线,根据等边三角形的性质得∠ACB=∠ABC=60°,由DG∥BC,得∠FGD=120°,∠GDC=120°,△AGD为等边三角形,而∠EDF=120°,得∠GDF=∠CDE,易证得△GDF∽△CDE,所以FG:CE=DG:DC,即CE:DC=FG:DG=FG:AG,设BF=x,AF=2x,则AB=3x,AG=1.5x,FG=1.5xx=0.5x,即可得到CE:CD的比值.
解:过D作DG∥BC交AB于G,如图,
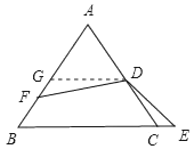
∵D是AC的中点,
∴DG为△ABC的中位线,
∵△ABC是等边三角形,
∴∠ACB=∠ABC=60°,
∴∠DCE=120°,
又∵DG∥BC,
∴∠FGD=120°,∠GDC=120°,△AGD为等边三角形,
∵∠EDF=120°,
∴∠GDF=∠CDE,
∴△GDF∽△CDE,
∴FG:CE=DG:CD,即CE:CD=FG:DG,
而DG=AG=BG,AF=2BF,
设BF=x,AF=2x,则AB=3x,AG=1.5x,FG=1.5xx=0.5x,
∴CE:CD=FG:DG=FG:AG=0.5x:1.5x=1:3.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在公路 MN 两侧分别有 A![]() , A
, A![]() ......A
......A![]() ,七个工厂,各工厂与公路 MN(图中粗线)之间有小公路连接.现在需要在公路 MN 上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( ).
,七个工厂,各工厂与公路 MN(图中粗线)之间有小公路连接.现在需要在公路 MN 上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( ).
①车站的位置设在 C 点好于 B 点;
②车站的位置设在 B 点与 C 点之问公路上任何一点效果一样;
③车站位置的设置与各段小公路的长度无关.
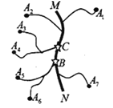
A.①B.②C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
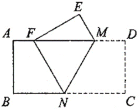
【题目】如图,矩形ABCD中,点M、N分别在AD、BC边上,将矩形ABCD沿MN翻折,点C恰好落在AD边上的点F处,若MD=1,∠MNC=60°,则AB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,二次函数y=x2﹣2mx+m2+2m+2的图象与x轴有两个交点.
(1)当m=﹣2时,求二次函数的图象与x轴交点的坐标;
(2)过点P(0,m﹣1)作直线1⊥y轴,二次函数图象的顶点A在直线l与x轴之间(不包含点A在直线l上),求m的范围;
(3)在(2)的条件下,设二次函数图象的对称轴与直线l相交于点B,求△ABO的面积最大时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,.过B作BE//AC.
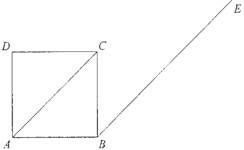
(1)求BE与AC之间的距离;
(2)F为BE上一点,连接AF,过C作CG//AF交BE于G.若∠FAB=15°,
①依题意补全图形;
②求证:四边形AFGC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠BAC的平分线AD交BC于点D,DE垂直平分AC,垂足为点E.
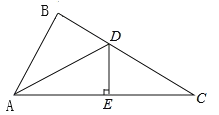
(1)证明∠BAD=∠C;
(2)∠BAD=29°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
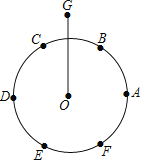
【题目】尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:
①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;
②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;
③连结OG.
问:OG的长是多少?
大臣给出的正确答案应是( )
A. ![]() r B. (1+
r B. (1+![]() )r C. (1+
)r C. (1+![]() )r D.
)r D. ![]() r
r
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1,将矩形纸片![]() 沿对角线
沿对角线![]() 剪开,得到
剪开,得到![]() 和
和![]() .并且量得
.并且量得![]() ,
,![]() .
.
操作发现:
(1)将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转
为旋转中心,按逆时针方向旋转![]() ,使
,使![]() ,得到如图2所示的
,得到如图2所示的![]() ,过点
,过点![]() 作
作![]() 的平行线,与
的平行线,与![]() 的延长线交于点
的延长线交于点![]() ,则四边形
,则四边形![]() 的形状是________.
的形状是________.
(2)创新小组将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转,使
为旋转中心,按逆时针方向旋转,使![]() 、
、![]() 、
、![]() 三点在同一条直线上,得到如图3所示的
三点在同一条直线上,得到如图3所示的![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 并延长至点
并延长至点![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() ,得到四边形
,得到四边形![]() ,发现它是正方形,请你证明这个结论.
,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将![]() 沿着
沿着![]() 方向平移,使点
方向平移,使点![]() 与点
与点![]() 重合,此时
重合,此时![]() 点平移至
点平移至![]() 点,
点,![]() 与
与![]() 相交于点
相交于点![]() ,如图4所示,连接
,如图4所示,连接![]() ,试求
,试求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县木瓜村盛产优种红富士苹果,曾推选参加省农产品博览会,某人去该地水果批发市场采购苹果,他看中了A、B两家苹果.这两家苹果品质都一样,市场售价都为6元/千克,但批发进价不相同.两家苹果批发进价如下:
A家规定:批发数量不超过1000千克,可按市场售价的92%优惠;批发数量多于1000千克但不超过2000千克,可全部按市场售价的90%优惠;批发数超过2000千克则全部按市场售价的88%优惠.
B家的规定如下表:
数量范围(千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上部分 |
批发进价(元) | 市场售价的95% | 市场售价的85% | 市场售价的75% | 市场售价的70% |
[表格说明: ![]() 家苹果批发进价按分段计算,如:某人要批发苹果2100千克,则批发进价
家苹果批发进价按分段计算,如:某人要批发苹果2100千克,则批发进价![]() ]
]
根据上述信息,请解答下列问题:
(1)如果此人要批发1000千克苹果,则他在![]() 家批发需要_______元,在
家批发需要_______元,在![]() 家批发需要_______元;
家批发需要_______元;
(2)如果此人批发![]() 千克苹果(1500<x<2000),则他在
千克苹果(1500<x<2000),则他在![]() 家批发需要_______元,在
家批发需要_______元,在![]() 家批发需要_______元(用含
家批发需要_______元(用含![]() 的代数式表示);
的代数式表示);
(3)现在此人要批发3000千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com