
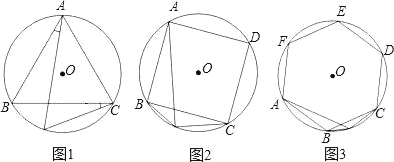
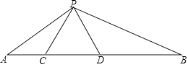
【题目】(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC.
下面给出一种证明方法,你可以按这一方法补全证明过程,也可以选择另外的证明方法.
证明:在AP上截取AE=CP,连接BE
∵△ABC是正三角形
∴AB=CB
∵∠1和∠2的同弧圆周角
∴∠1=∠2
∴△ABE≌△CBP
(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:PA=PC+ ![]() PB.
PB.
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,直接写出结论.
【答案】(1)见解析;(2)见解析;(3)PA=PC+![]() PB
PB
【解析】
(1)延长BP至E,使PE=PC,连接CE,证明△PCE是等边三角形.利用CE=PC,∠E=∠3=60°,∠EBC=∠PAC,得到△BEC≌△APC,所以PA=BE=PB+PC;
(2)过点B作BE⊥PB交PA于E,证明ABE≌△CBP,所以PC=AE,可得PA=PC+![]() PB;(3)在AP上截取AQ=PC,连接BQ可证△ABQ≌△CBP,所以BQ=BP.又因为∠APB=30°.所以PQ=
PB;(3)在AP上截取AQ=PC,连接BQ可证△ABQ≌△CBP,所以BQ=BP.又因为∠APB=30°.所以PQ=![]() PB,PA=PQ+AQ=
PB,PA=PQ+AQ=![]() PB+PC.
PB+PC.
证明:(1)延长BP至E,使PE=PC,
连接CE.∵∠1=∠2=60°,∠3=∠4=60°,
∴∠CPE=60°,
∴△PCE是等边三角形,
∴CE=PC,∠E=∠3=60°;
又∵∠EBC=∠PAC,
∴△BEC≌△APC,
∴PA=BE=PB+PC.
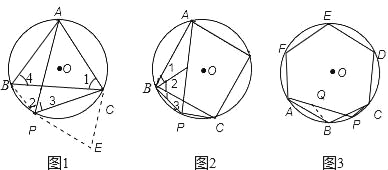
(2)过点B作BE⊥PB交PA于E.
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
又∵∠APB=45°,
∴BP=BE,∴;![]()
又∵AB=BC,
∴△ABE≌△CBP,
∴PC=AE.
∴![]() .
.
(3)答:![]() ;
;
证明:在AP上截取AQ=PC,
连接BQ,∵∠BAP=∠BCP,AB=BC,
∴△ABQ≌△CBP,
∴BQ=BP.
又∵∠APB=30°,
∴![]() PB
PB
∴![]() PB+PC
PB+PC


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
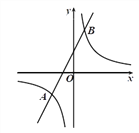
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 与反比例函数
与反比例函数![]() 交于点
交于点![]() ,
, ![]() .
.
(1)分别求出反比例函数和一次函数的表达式;
(2)根据函数图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走.
(1)假如每天能运x立方米,所需时间为y天,写出y与x之间的函数解析式(不要求写出自变量的取值范围);
(2)若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的条件下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
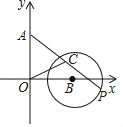
【题目】如图,在平面直角坐标系中,A(0,3)、B(3,0),以点B为圆心、2为半径的⊙B上有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为( )
A. 1 B. 2![]() ﹣1 C.
﹣1 C. ![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 、
、![]() 在边
在边![]() 上,
上,![]() ,
,![]() .
.
![]() 试说明
试说明![]() 与
与![]() 相似.
相似.
![]() 若
若![]() ,
,![]() ,
,![]() ,请你求出
,请你求出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
![]() 小明猜想:若
小明猜想:若![]() ,
,![]() ,
,![]() ,只要
,只要![]() 与
与![]() 之间满足某种关系式,问题
之间满足某种关系式,问题![]() 中的函数关系式仍然成立.你同意小明的观点吗?如果你同意,请求出
中的函数关系式仍然成立.你同意小明的观点吗?如果你同意,请求出![]() 与
与![]() 所满足的关系式;若不同意,请说明理由.
所满足的关系式;若不同意,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
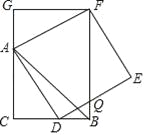
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQAC,其中正确的结论的个数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
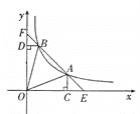
【题目】如图,直线y=-x+b与双曲线y=![]() (x>0)交于A、B两点,与x轴、y轴分别交干E、F两点,AC⊥x轴于点C,BD⊥y轴于点D,当b= _____时,△ACE、△BDF与△ABO面积的和等于△EFO面积的
(x>0)交于A、B两点,与x轴、y轴分别交干E、F两点,AC⊥x轴于点C,BD⊥y轴于点D,当b= _____时,△ACE、△BDF与△ABO面积的和等于△EFO面积的![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com