
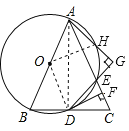
【题目】如图,在△ABC中,AB=AC=10,以AB为直径的OO与BC相交于点D,与AC相交于点E,DF⊥AC,垂足为F,连接DE,过点A作AG⊥DE,垂足为G,AG与⊙O交于点H.
(1)求证:DF是⊙O的切线;
(2)若∠CAG=25°,求弧AH的长;
(3)若tan∠CDF=![]() ,求AE的长;
,求AE的长;

【答案】(1)证明见解析(2)![]() (3)6
(3)6
【解析】
(1)连接OD、AD,根据圆周角定理得到∠ADB=90°,求得OD∥AC,根据平行线的性质得到OD⊥DF,根据切线的判定定理即可得到结论;
(2)连接OH,根据三角形的内角和得到∠AEG=65°,求得∠B=∠AEG=65°,求得∠AOH=30°,根据弧长公式即可得到结论;
(3)根据余角的性质得到∠CAD=∠CDF,求出tan∠CAD=tan∠CDF=![]() ,根据勾股定理得到CD=2
,根据勾股定理得到CD=2![]() ,根据相似三角形的性质得到CF=2,于是得到结论.
,根据相似三角形的性质得到CF=2,于是得到结论.
(1)证明:连接OD、AD,
AB是⊙O的半径,
∴∠ADB=90°,
∵AB=AC,
∵点D是BC的中点,O是AB的中点,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
∵OD是⊙O的半径,
DF是⊙O的切线;
(2)解:连接OH,
∵AG⊥DG,∴∠G=90°,
∵∠CAG=25°,
∴∠AEG=65°,
∴∠B=∠AEG=65°,
∴∠BAC=180°﹣65°﹣65°=50°,
∴∠OAH=75°,
∴∠AOH=30°,
∴l弧AH=![]() ;
;
(3)解:∵∠CAD+∠C=90°,∠CDF+∠C=90°,
∴∠CAD=∠CDF,
∴tan∠CAD=tan∠CDF=![]() ,
,
∴AD=2CD,
∴DC2+(2CD)2=102,
∴CD=2![]() ,
,
∵△CDF∽△CAD,
∴DC2=CFAC,
∴CF=2,
∴CD=DE,
∵OF⊥AC,
∴EF=CF=2,
∴AE=10﹣2﹣2=6.


科目:初中数学 来源: 题型:
【题目】随着新能源汽车的发展,某公交公司将用新能源公交车淘汰某一条线路上“冒黑烟”较严重的燃油公交车,计划购买A型和B型新能源公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需300万元;若购买A型公交车2辆,B型公交车1辆,共需270万元,
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1000万元,且确保这10辆公交车在该线路的年均载客量总和不少于900万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
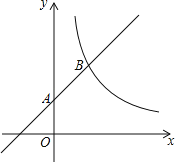
【题目】如图,在平面直角坐标系中,一次函数y=x+b的图象经过点A(0,1),与反比例函数y=![]() (x>0)的图象交于B(m,2).
(x>0)的图象交于B(m,2).
(1)求k和b的值;
(2)在双曲线y=![]() (x>0)上是否存在点C,使得△ABC为等腰直角三角形?若存在,求出点C坐标;若不存在,请说明理由.
(x>0)上是否存在点C,使得△ABC为等腰直角三角形?若存在,求出点C坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
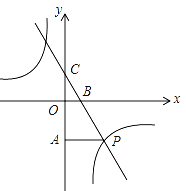
【题目】如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数![]() 的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18.
的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18.
(1)求上述一次函数与反比例函数的表达式;
(2)设Q是一次函数y=kx+3图象上的一点,且满足△OCQ的面积是△BCO面积的2倍,求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
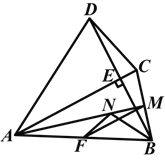
【题目】(2014山东淄博)如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
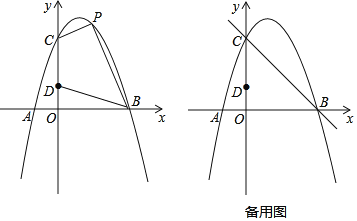
【题目】如图,对称轴为直线x=1的抛物线经过A(﹣1,0)、C(0,3)两点,与x轴的另一个交点为B,点D在y轴上,且OB=3OD
(1)求该抛物线的表达式;
(2)设该抛物线上的一个动点P的横坐标为t
①当0<t<3时,求四边形CDBP的面积S与t的函数关系式,并求出S的最大值;
②点Q在直线BC上,若以CD为边,点C、D、Q、P为顶点的四边形是平行四边形,请求出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠AOB=,反比例函数y=(k>0)在第一象限内的图象经过点A,与BC交于点F.

(1)若OA=10,求反比例函数解析式;
(2)若点F为BC的中点,且△AOF的面积S=12,求OA的长和点C的坐标;
(3)在(2)中的条件下,过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
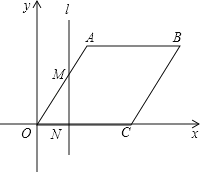
【题目】如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).
(1)求A、B两点的坐标;
(2)设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;
(3)在题(2)的条件下,是否存在某一时刻,使得△OMN的面积与OABC的面积之比为3:4?如果存在,请求出t的取值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() 是常数)经过点
是常数)经过点![]() .
.
(1)求该抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点,![]() 关于原点的对称点为
关于原点的对称点为![]() .
.
①当点![]() 落在该抛物线上时,求
落在该抛物线上时,求![]() 的值;
的值;
②当点![]() 落在第二象限内,
落在第二象限内,![]() 取得最小值时,求
取得最小值时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com