练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】求1+2+22+23+…+22016的值，可设S=1+2+22+23+…+22016 ， 于是2S=2+22+23+…+22017 ， 因此2S﹣S=22017﹣1，所以S=22017﹣1．我们把这种求和方法叫错位相减法．仿照上述的思路方法，计算出1+5+52+53+…+52016的值为（ ）
    A.52017﹣1
    B.52016﹣1
    C.
    D.

    【答案】C
    【解析】解：设S=1+5+52+53+…+52016 ， 则5S=5+52+53+…+52017 ，
    ∴5S﹣S=52017﹣1，
    ∴S= ．
    故选C．
    【考点精析】本题主要考查了数与式的规律的相关知识点，需要掌握先从图形上寻找规律，然后验证规律，应用规律，即数形结合寻找规律才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知一张纸片ABCD，∠B＞90°，点E是AB的中点，点G是BC上的一个动点，沿BG将纸片折叠，使点B落在纸片上的点F处，连接AF，则下列各角中与∠BEG不一定相等的是（ ）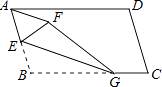
    A.∠FEG
    B.∠EAF
    C.∠AEF
    D.∠EFA

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若a＝2016×2018－2016×2017， b＝2015×2016－2013×2017，，则a，b，c的大小关系是( )

    A. a＜b＜c B. a＜c＜b C. b＜a＜c D. b＜c＜a

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】请观察下列算式，找出规律并填空。

    ，，，···

    根据以上规律解答以下三题：

    (1) 第10个等式是:__________=_____________

    第n个等式是:__________=_____________

    (2)计算： 的值。

    (3)若有理数满足 ,试求： 的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】大家知道，它在数轴上表示5的点与原点(即表示0的点)之间的距离.又如式子,它在数轴上的意义是表示6的点与表示3的点之间的距离.即点A、B在数轴上分别表示数a、b,则A、B两点的距离可表示为:|AB|=.根据

    以上信息，回答下列问题：

    (1)数轴上表示2和5的两点之间的距离是 ；数轴上表示-2和-5的两点之间的距离是 .

    （2）点A、B在数轴上分别表示实数x和.

    ①用代数式表示A、B两点之间的距；

    ②如果,求x的值.

    （3）直接写出代数式的最小值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，老王开车从A到D，全程共72千米．其中AB段为平地，车速是30千米/小时，BC段为上山路，车速是22.5千米/小时，CD段为下山路，车速是36千米/小时，已知下山路是上山路的2倍．

    （1）若AB=6千米，老王开车从A到D共需多少时间？

    （2）当BC的长度在一定范围内变化时，老王开车从A到D所需时间是否会改变？为什么？（给出计算过程）

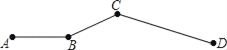
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】每个小方格是边长为1个单位长度的小正方形，菱形OABC在平面直角坐标系的位置如图所示．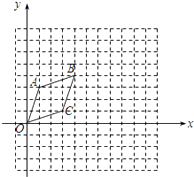
    （I）以O为位似中心，在第一象限内将菱形OABC放大为原来的2倍得到菱形OA1B1C1 ， 请画出菱形OA1B1C1 ， 并直接写出点B1的坐标；
    （II）将菱形OABC绕原点O顺时针旋转90°菱形OA2B2C2 ， 请画出菱形OA2B2C2 ， 并求出点B旋转到点B2的路径长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线经过点A（﹣2，0），B（﹣3，3）及原点O，顶点为C．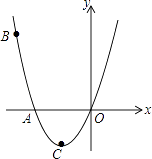
    （1）求抛物线的函数解析式；
    （2）连接BC交x轴于点F．试在y轴负半轴上找一点P，使得△POC∽△BOF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知等边△ABC．
    （1）如图①，P为等边△ABC外一点，且∠BPC=120°，试猜想线段BP、PC、AP之间的数量关系，并证明你的猜想；
    （2）如图②，P为等边△ABC内一点，且∠APD=120°，求证：PA+PD+PC＞BD；
    （3）在（2）的条件下，若∠CPD=30°，AP=4，CP=5，DP=8，求BD的长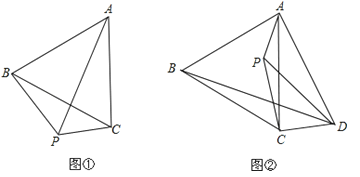

    查看答案和解析>>

    同步练习册答案