
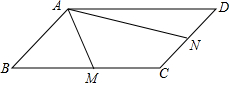
 如图,在平行四边形ABCD中,M、N分别为BC、CD的中点,AM=1,AN=2,∠MAN=60°,则AB的长为$\frac{4}{3}$.
如图,在平行四边形ABCD中,M、N分别为BC、CD的中点,AM=1,AN=2,∠MAN=60°,则AB的长为$\frac{4}{3}$. 分析 延长DC和AM交于E,过点E作EH⊥AN于点H,易证得△ABM≌△ECM,即可得AB=$\frac{2}{3}$NE,然后由AM=1,AN=2,且∠MAN=60°,求得AH,NH与EH的长,继而求得EN的长,则可求得答案.
解答 解:延长DC和AM交于E,过点E作EH⊥AN于点H,如图.
∵四边形ABCD为平行四边形,
∴AB∥CE,
∴∠BAM=∠CEM,∠B=∠ECM.
∵M为BC的中点,
∴BM=CM.
在△ABM和△ECM中,$\left\{\begin{array}{l}{∠BAM=∠CEN}&{\;}\\{∠B=∠ECM}&{\;}\\{BM=CM}&{\;}\end{array}\right.$,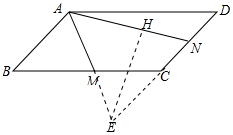
∴△ABM≌△ECM(AAS),
∴AB=CD=CE,AM=EM=4,
∵N为边DC的中点,
∴NE=3NC=$\frac{3}{2}$AB,即AB=$\frac{2}{3}$NE,
∵AN=2,AE=2AM=2,且∠MAN=60°,
∴∠AEH=30°,
∴AH=$\frac{1}{2}$AE=1,
∴EH=$\sqrt{A{E}^{2}-A{H}^{2}}$=$\sqrt{3}$,
∴NH=AN-AH=2-1=1,
∴EN=$\sqrt{N{H}^{2}+E{H}^{2}}$=2,
∴AB=$\frac{2}{3}$×2=$\frac{4}{3}$;
故答案为:$\frac{4}{3}$.
点评 此题考查了平行四边形的性质、全等三角形的判定与性质以及勾股定理.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 0,-1或1 | C. | 1或-1 | D. | 0或1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
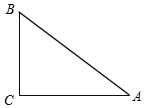 在Rt△ABC中,∠C=90°,AC=4,BC=3,
在Rt△ABC中,∠C=90°,AC=4,BC=3,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
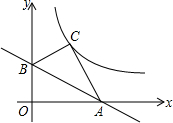 如图,已知点A(6,0),B(0,2$\sqrt{3}$),O为坐标原点,点O关于直线AB的对称点C恰好落在反比例函数y=$\frac{k}{x}$(k>0)的图象上,求k的值.
如图,已知点A(6,0),B(0,2$\sqrt{3}$),O为坐标原点,点O关于直线AB的对称点C恰好落在反比例函数y=$\frac{k}{x}$(k>0)的图象上,求k的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 序号 | 范围(单位:秒) | 频数 | 频率 |
| 1 | 170<x≤200 | 5 | 0.1 |
| 2 | 200<x≤230 | 13 | a |
| 3 | 230<x≤260 | 15 | 0.3 |
| 4 | 260<x≤290 | c | d |
| 5 | 290<x≤320 | 5 | 0.1 |
| 6 | 320<x≤350 | 2 | 0.04 |
| 7 | 350<x≤380 | 2 | 0.04 |
| 合计 | b | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
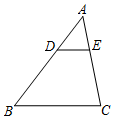 如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E,如果$\frac{AE}{EC}$=$\frac{1}{2}$,DE=7,那么BC的长为21.
如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E,如果$\frac{AE}{EC}$=$\frac{1}{2}$,DE=7,那么BC的长为21.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com