
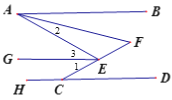
【题目】如图,已知AB∥HD,EG平分∠AEC,EG∥AB,AF平分∠BAE,CE的延长线交AF于点F,若∠HCE=![]() °,∠F=
°,∠F=![]() °,用含
°,用含![]() 的代数式表示
的代数式表示![]() ,则
,则![]() =_______
=_______

【答案】270-![]() x
x
【解析】
由角平分线定义可得∠AEC=2∠1,∠1=∠3,∠2=![]() ∠EAB,由AB∥HD, EG∥AB,可得∠BAE=∠3,EG//HD,继而可得∠1、∠AEC、∠2,再由三角形外角的性质可知∠2+∠F=∠AEC,代入相关式子即可求得答案.
∠EAB,由AB∥HD, EG∥AB,可得∠BAE=∠3,EG//HD,继而可得∠1、∠AEC、∠2,再由三角形外角的性质可知∠2+∠F=∠AEC,代入相关式子即可求得答案.
∵EG平分∠AEC, AF平分∠BAE,
∴∠AEC=2∠1,∠1=∠3,∠2=![]() ∠EAB,
∠EAB,
∵AB∥HD, EG∥AB,
∴∠BAE=∠3,EG//HD,
∴∠1=180°-∠HCE=180°-x°,
∴∠AEC=2(180°-x°),∠2=![]() (180°-x°),
(180°-x°),
∵∠2+∠F=∠AEC,
∴![]() (180°-x°)+y°=2(180°-x°),
(180°-x°)+y°=2(180°-x°),
∴y=270-![]() x,
x,
故答案为:270-![]() x.
x.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
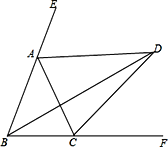
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④BD平分∠ADC;⑤∠BDC=![]() ∠BAC.
∠BAC.
其中正确的结论有( )
A. 5个 B. 4个
C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
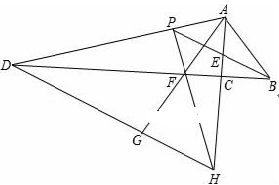
【题目】如图,Rt△ACB中,∠ACB=90°,∠ABC的平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD﹣AH=AB;④DG=AP+GH.其中正确的是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红家有一块L形的菜地,要把L形的菜地按如图所示分成两块面积相等的梯形,种上不同的蔬菜.这两个梯形的上底都是a m,下底都是b m,高都是(b-a) m.
(1)求小红家这块L形菜地的面积.(用含a、b的代数式表示)
(2)若a2+b2=15,ab=5,求小红家这块L形菜地的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:对于形如![]() 这样的二次三项式,可以用公式法将它分解成
这样的二次三项式,可以用公式法将它分解成![]() 的形式.但对于二次三项式
的形式.但对于二次三项式![]() ,就不能直接运用公式了.此时,我们可以在二次三项式
,就不能直接运用公式了.此时,我们可以在二次三项式![]() 中先加上一项
中先加上一项![]() ,使它与
,使它与![]() 的和成为一个完全平方式,再减去
的和成为一个完全平方式,再减去![]() ,整个式子的值不变,于是有:
,整个式子的值不变,于是有:![]()
![]()
![]()
![]()
像这样,先添一适当项,使式中出现完全平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”,利用“配方法",解决下列问题:
(1)分解因式:![]() .
.
(2)比较代数式![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中, A、B两点分别在x轴、y轴的正半轴上,且OB = OA=3.(1)、求点A、B的坐标;(2)、已知点C(-2,2),求△BOC的面积;(3)、点P是第一象限角平分线上一点,若![]() ,求点P的坐标.
,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A,B两点分别在x轴和y轴上,OA=1,OB= ![]() ,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1 , 连接A1B1 , 再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 .
,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1 , 连接A1B1 , 再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 . 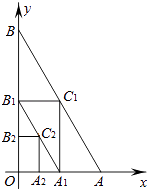
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一蓄水池有水40m3,按一定的速度放水,水池里的水量y (m3)与放水时间t(分)有如下关系:
放水时间(分) | 1 | 2 | 3 | 4 | ... |
水池中水量(m) | 38 | 36 | 34 | 32 | ... |
下列结论中正确的是
A. y随t的增加而增大B. 放水时间为15分钟时,水池中水量为8m3
C. 每分钟的放水量是2m3D. y与t之间的关系式为y=38-2t
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com