
【题目】生活与数学

(1)吉姆同学在某月的日历上利用图1的正方形方框圈出2×2个数,四个数的和是32,那么这四个数是_______________.
(2)玛丽在上面的日历上利用图2的斜框图圈出2×2个数,四个数的和是46,则它们分别是__________.
(3)莉莉也在日历上利用图3的十字框形圈出5个数,它们的和是50,则中间的数是__________.
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是________号.
【答案】4,5,11,12 8,9,14,15 10 29
【解析】
(1)先根据日历上的数据规律把所要求的数用代数式表示,用一元一次方程求解即可;
(2)先根据日历上的数据规律把所要求的数用代数式表示,用一元一次方程求解即可;
(3)先根据日历上的数据规律把所要求的数用代数式表示,用一元一次方程求解即可;
(4)先设最后一个星期日是x,根据日历上的数据规律把所要求的数用代数式表示,用一元一次方程求解即可.
(1)设第一个数是x,其他的数为x+1,x+7,x+8,则
x+x+1+x+7+x+8=32,
解得:x=4;∴这四个数是:4,5,11,12.
故答案为:4,5,11,12;
(2)设第一个数是x,其他的数为x+1,x+6,x+7,则
x+x+1+x+6+x+7=46,
解得:x=8.
x+1=9,x+6=14,x+7=15.
故答案为:8,9,14,15;
(3)设中间的数是x,则
5x=50,
解得:x=10.
故答案为:10;
(4)设最后一个星期日是x,则其它4个星期日分别是x﹣7,x﹣14,x﹣21,x﹣28,则
x+x﹣7+x﹣14+x﹣21+x﹣28=75,
解得:x=29.
故答案为:29.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.现将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2018次,点B的落点依次为![]() ,
,![]() ,
,![]() ,
,![]() , ……,则
, ……,则![]() 的坐标为________________.
的坐标为________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0), B(0,﹣1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,矩形ABCD的顶点A、B分别在OM、ON上,当B在边ON上运动时,A 随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,则运动过程中,点C到点O的最大距离为___________.
,矩形ABCD的顶点A、B分别在OM、ON上,当B在边ON上运动时,A 随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,则运动过程中,点C到点O的最大距离为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a、c满足|a+2|+(c﹣7)2=0.
(1)a= ,b= ,c= ;
(2)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ;AC= ;BC= ;(用含t的代数式表示)
(3)请问:3AC﹣5AB的值是否随着时间t的变化而改变?若变化,请说明理由:若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励节约用水,某地推行阶梯式水价计费制,标准如下:每月用水不超过17立方米的按每立方米![]() 元计费,超过17立方米而未超过30立方米的部分按每立方米
元计费,超过17立方米而未超过30立方米的部分按每立方米![]() 元计费,超过30立方米的部分按每立方米
元计费,超过30立方米的部分按每立方米![]() 元计费,某户居民上月用水35立方米,应缴水费_________元.
元计费,某户居民上月用水35立方米,应缴水费_________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A20的坐标为 ( )
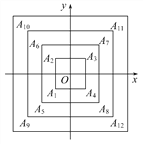
A. (5,5) B. (5,-5) C. (-5,5) D. (-5,-5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺,9,3分)正方形ABCD边长为1,E、F、G、H分别为边AB、BC、CD、DA上的点,且AE=BF=CG=DH.设小正方形EFGH的面积为y,AE=x. 则y关于x的函数图象大致是( )

A. B. C. D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进货价为每件30元,为了合理定价,先投放市场试销.据市场调查,销售价为每件40元时,每周的销售量是180件,而销售价每上涨1元,则每周的销售量就会减少5件,设每件商品的销售价上涨x元,每周的销售利润为y元.
(1)用含x的代数式表示:每件商品的销售价为 元,每件商品的利润为 元,每周的商品销售量为 件;
(2)求y关于x的函数关系式(不要求写出x的取值范围);
(3)应怎样确定销售价,使该商品的每周销售利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com