【答案】
分析:(1)连接AC,由于BC与⊙A相切,则AC⊥BC,在Rt△ABC中,OC⊥AB,根据射影定理即可求得OC的长,从而得到C点的坐标,进而用待定系数法求出直线BC的解析式.
(2)可设出G点的坐标(设横坐标,利用直线BC的解析式表示纵坐标),连接AP、AG;由于GC、GP都是⊙A的切线,那么∠AGC=∠ABP=60°,在Rt△AGC中,AC的长易求得,根据∠AGC的度数,即可求得AG的长;过G作GH⊥x轴于H,在Rt△GAH中,可根据G点的坐标表示出AH、GH的长,进而由勾股定理求得G点的坐标.
(3)若⊙A与直线交于点E、F,则AE=AF,如果△AEF是直角三角形,则∠EAF必为直角,那么△EAF是以A为顶点的等腰直角三角形,因此可分作两种情况考虑:
①点A在B点右侧时,可过A作直线BC的垂线,设垂足为M,在(2)题已经求得了⊙A的半径,即可得到AM的长,易证得△BAM∽△BCO,通过相似三角形所得比例线段即可求得AB的长,进而可得到OA的长,从而得出A点的坐标;
②点A在B点左侧时,方法同①.
解答:
解:(1)如图1所示,连接AC,则AC=

,
在Rt△AOC中,AC=
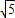
,OA=1,则OC=2,
∴点C的坐标为(0,2);
设切线BC的解析式为y=kx+b,它过点C(0,2),B(-4,0),
则有

,解之得
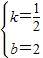
;
∴

.(4分)
(2)如图1所示,设点G的坐标为(a,c),过点G作GH⊥x轴,垂足为H点,
则OH=a,GH=c=

a+2,(5分)
连接AP,AG;
因为AC=AP,AG=AG,所以Rt△ACG≌Rt△APG(HL),
所以∠AGC=

×120°=60°,
在Rt△ACG中,∠AGC=60°,AC=

,
∴sin60°=

,∴AG=

;(6分)
在Rt△AGH中,AH=OH-OA=a-1,GH=

a+2,
∵AH
2+GH
2=AG
2,
∴(a-1)
2+

=

,
解之得:a
1=

,a
2=-

(舍去);(7分)
∴点G的坐标为(
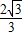
,
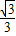
+2).(8分)

(3)如图2所示,在移动过程中,存在点A,使△AEF为直角三角形.(9分)
要使△AEF为直角三角形,∵AE=AF,
∴∠AEF=∠AFE≠90°,∴只能是∠EAF=90°;
当圆心A在点B的右侧时,过点A作AM⊥BC,垂足为点M,
在Rt△AEF中,AE=AF=

,
则EF=

,AM=

EF=


;
在Rt△OBC中,OC=2,OB=4,则BC=2

,
∵∠BOC=∠BMA=90°,∠OBC=∠OBM,
∴△BOC∽△BMA,
∴
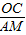
=

,
∴AB=

,
∴OA=OB-AB=4-
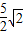
,
∴点A的坐标为(-4+

,0);(11分)
当圆心A在点B的左侧时,设圆心为A′,过点A′作A′M′⊥BC于点M′,可得:
△A′M′B≌△AMB,A′B=AB=

,
∴OA′=OB+A′B=4+

,
∴点A′的坐标为(-4-
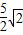
,0);
综上所述,点A的坐标为(-4+

,0)或(-4-
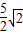
,0).(13分)
点评:此题考查的知识点有:一次函数解析式的确定、勾股定理、切线的性质、切线长定理、全等三角形及相似三角形的判定和性质等;需要注意的是(3)题中,一定要考虑到点A在B点左侧时的情况,以免漏解.

 ,过点C作⊙A的切线交x轴于点B(-4,0).
,过点C作⊙A的切线交x轴于点B(-4,0).
 解:(1)如图1所示,连接AC,则AC=
解:(1)如图1所示,连接AC,则AC= ,
,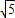 ,OA=1,则OC=2,
,OA=1,则OC=2, ,解之得
,解之得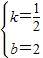 ;
; .(4分)
.(4分) a+2,(5分)
a+2,(5分) ×120°=60°,
×120°=60°, ,
, ,∴AG=
,∴AG= ;(6分)
;(6分) a+2,
a+2, =
= ,
, ,a2=-
,a2=- (舍去);(7分)
(舍去);(7分)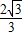 ,
,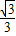 +2).(8分)
+2).(8分) (3)如图2所示,在移动过程中,存在点A,使△AEF为直角三角形.(9分)
(3)如图2所示,在移动过程中,存在点A,使△AEF为直角三角形.(9分) ,
, ,AM=
,AM= EF=
EF=
 ;
; ,
,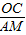 =
= ,
, ,
,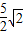 ,
, ,0);(11分)
,0);(11分) ,
, ,
,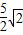 ,0);
,0); ,0)或(-4-
,0)或(-4-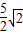 ,0).(13分)
,0).(13分)

 口算能手系列答案
口算能手系列答案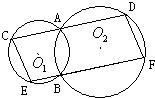 21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.
21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.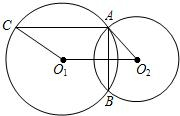 ,⊙O2的半径为
,⊙O2的半径为 (1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D.
(1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D.