
【题目】如图1,二次函数y=ax2﹣3ax﹣4a的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,﹣3).
(1)求二次函数的表达式及点A、点B的坐标;
(2)若点D在二次函数图象上,且![]() ,求点D的横坐标;
,求点D的横坐标;
(3)将直线BC向下平移,与二次函数图象交于M,N两点(M在N左侧),如图2,过M作ME∥y轴,与直线BC交于点E,过N作NF∥y轴,与直线BC交于点F,当MN+ME的值最大时,求点M的坐标.
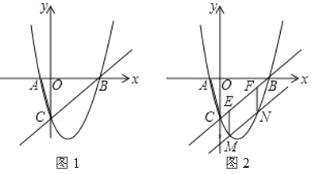
【答案】(1)y=![]() ,A(﹣1,0),B(4,0);(2)2+2
,A(﹣1,0),B(4,0);(2)2+2![]() 或2﹣2
或2﹣2![]() 或2;(3)M(
或2;(3)M(![]() ,﹣
,﹣![]() )
)
【解析】
(1)求出a,即可求解;
(2)求出直线BC的解析式,过点D作DH∥y轴,与直线BC交于点H,根据三角形面积的关系求解;
(3)过点M作MG∥x轴,交FN的延长线于点G,设M(m,![]() m-3),N(n,
m-3),N(n,![]() n2-
n2-![]() n-3),判断四边形MNFE是平行四边形,根据ME=NF,求出m+n=4,再确定ME+MN=-
n-3),判断四边形MNFE是平行四边形,根据ME=NF,求出m+n=4,再确定ME+MN=-![]() m2+3m+5-
m2+3m+5-![]() m=-
m=-![]() (m-
(m-![]() )2+
)2+![]() ,即可求M;
,即可求M;
(1)y=ax2﹣3ax﹣4a与y轴交于点C(0,﹣3),
∴a=![]() ,
,
∴y=![]() ,
,
与x轴交点A(﹣1,0),B(4,0);
(2)设直线BC的解析式为y=kx+b,
∴![]() ,
,
∴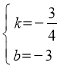 ,
,
∴y=![]() x﹣3;
x﹣3;
过点D作DH∥y轴,与直线BC交于点H,
设H(x,![]() x﹣3),D(x,
x﹣3),D(x,![]() x2﹣
x2﹣![]() x﹣3),
x﹣3),
∴DH=|![]() x2﹣3x|,
x2﹣3x|,
∵S△ABC=![]()
![]() ,
,
∴S△DBC=![]() =6,
=6,
∴S△DBC=2×|![]() x2﹣3x|=6,
x2﹣3x|=6,
∴x=2+2![]() ,x=2﹣2
,x=2﹣2![]() ,x=2;
,x=2;
∴D点的横坐标为2+2![]() ,2﹣2
,2﹣2![]() ,2;
,2;
(3)过点M作MG∥x轴,交FN的延长线于点G,
设M(m,![]() m2﹣
m2﹣![]() m﹣3),N(n,
m﹣3),N(n,![]() n2﹣
n2﹣![]() n﹣3),
n﹣3),
则E(m,![]() m﹣3),F(n,
m﹣3),F(n,![]() n﹣3),
n﹣3),
∴ME=﹣![]() m2+3m,NF=﹣
m2+3m,NF=﹣![]() n2+3n,
n2+3n,
∵EF∥MN,ME∥NF,
∴四边形MNFE是平行四边形,
∴ME=NF,
∴﹣![]() m2+3m=﹣
m2+3m=﹣![]() n2+3n,
n2+3n,
∴m+n=4,
∴MG=n﹣m=4﹣2m,
∴∠NMG=∠OBC,
∴cos∠NMG=cos∠OBC=![]() ,
,
∵B(4,0),C(0,﹣3),
∴OB=4,OC=3,
在Rt△BOC中,BC=5,
∴MN=![]() (n﹣m)=
(n﹣m)=![]() (4﹣2m)=5﹣
(4﹣2m)=5﹣![]() m,
m,
∴ME+MN=﹣![]() m2+3m+5﹣
m2+3m+5﹣![]() m=﹣
m=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴当m=![]() 时,ME+MN有最大值,
时,ME+MN有最大值,
∴M(![]() ,﹣
,﹣![]() )
)


科目:初中数学 来源: 题型:
【题目】(感知)如图①,点C是AB中点,CD⊥AB,P是CD上任意一点,由三角形全等的判定方法“SAS”易证△PAC≌△PBC,得到线段垂直平分线的一条性质“线段垂直平分线上的点到线段两端的距离相等”

(探究)如图②,在平面直角坐标系中,直线y=-![]() x+1分别交x轴、y轴于点A和点B,点C是AB中点,CD⊥AB交OA于点D,连结BD,求BD的长
x+1分别交x轴、y轴于点A和点B,点C是AB中点,CD⊥AB交OA于点D,连结BD,求BD的长
(应用)如图③
(1)将线段AB绕点A顺时针旋转90°得到线段AB′,请在图③网格中画出线段AB;
(2)若存在一点P,使得PA=PB′,且∠APB′≠90°,当点P的横、纵坐标均为整数时,则AP长度的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)根据题意,填写下表:
重量(千克) 费用(元) | 0.5 | 1 | 3 | 4 | … |
甲公司 | _________ | 22 | _________ | 67 | … |
乙公司 | 11 | ________ | 51 | _________ | … |
(2)请分别写出甲乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(3)小明应选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.
(一)猜测探究
在△ABC中,AB=AC,M是平面内任意一点,将线段AM绕点A按顺时针方向旋转与∠BAC相等的角度,得到线段AN,连接NB.
(1)如图1,若M是线段BC上的任意一点,请直接写出∠NAB与∠MAC的数量关系是_______,NB与MC的数量关系是_______;
(2)如图2,点E是AB延长线上点,若M是∠CBE内部射线BD上任意一点,连接MC,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由。
(二)拓展应用
如图3,在△A1B1C1中,A1B1=8,∠A1B1C1=90°,∠C1=30°,P是B1C1上的任意点,连接A1P,将A1P绕点A1按顺时针方向旅转60°,得到线段A1Q,连接B1Q.求线段B1Q长度的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年4月22日是第50个世界地球日,某校在八年级5个班中,每班各选拔10名学生参加“环保知识竞赛”并评出了一、二、三等奖各若干名,学校将获奖情况绘成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
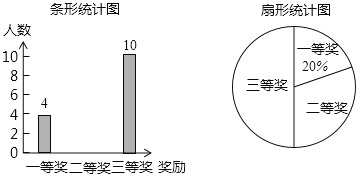
(1)求本次竞赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)已知甲、乙、丙、丁4位同学获得一等奖,学校将采取随机抽签的方式在4人中选派2人参加上级团委组织的“爱护环境、保护地球”知识竞赛,请求出抽到的2人恰好是甲和乙的概率(用画树状图或列表等方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发市场经销龟苓膏粉,其中![]() 品牌的批发价是每包20元,
品牌的批发价是每包20元,![]() 品牌的批发价是每包25元,小明计划购买这两种品牌的龟苓膏粉共1000包,解答下列问题:
品牌的批发价是每包25元,小明计划购买这两种品牌的龟苓膏粉共1000包,解答下列问题:
(1)若购买这些龟苓膏粉共花费22000元,求两种品牌的龟苓膏粉各购买了多少包?
(2)若凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元,
若购买会员卡并用此卡购买这些龟苓膏粉共花费![]() 元,设
元,设![]() 品牌购买了
品牌购买了![]() 包,请求出
包,请求出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
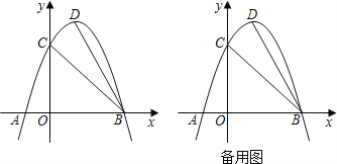
【题目】 如图,抛物线y=-x2+bx+c与x轴交于A、B两点,交y轴正半轴于C点,D为抛物线的顶点,A(-1,0),B(3,0).
(1)求出二次函数的表达式.
(2)点P在x轴上,且∠PCB=∠CBD,求点P的坐标.
(3)在x轴上方抛物线上是否存在一点Q,使得以Q,C,B,O为顶点的四边形被对角线分成面积相等的两部分?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 是由抛物线
是由抛物线![]() :
:![]() 平移得到的,并且
平移得到的,并且![]() 的顶点为(1,-4)
的顶点为(1,-4)
(1)求![]() 的值;
的值;
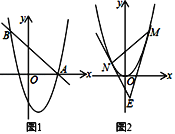
(2)如图1,抛物线C1与x轴正半轴交于点A,直线![]() 经过点A,交抛物线C1于另一点B.请你在线段AB上取点P,过点P作直线PQ∥y轴交抛物线C1于点Q,连接AQ.
经过点A,交抛物线C1于另一点B.请你在线段AB上取点P,过点P作直线PQ∥y轴交抛物线C1于点Q,连接AQ.
①若AP=AQ,求点P的坐标;
②若PA=PQ,求点P的横坐标.
(3)如图2,△MNE的顶点M、N在抛物线C2上,点M在点N右边,两条直线ME、NE与抛物线C2均有唯一公共点,ME、NE均与y轴不平行.若△MNE的面积为16,设M、N两点的横坐标分别为m、n,求m与n的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则下列说法正确的是( )
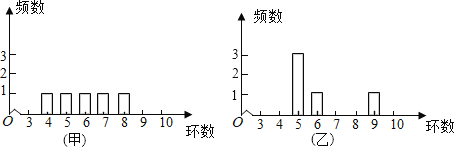
A.甲的成绩的平均数小于乙的成绩的平均数
B.甲的成绩的中位数等于乙的成绩的中位数
C.甲的成绩的极差小于乙的成绩的极差
D.甲的成绩的方差小于乙的成绩的方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com