
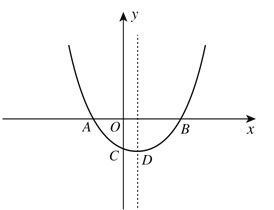
【题目】如图,抛物线![]() (a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.
(a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.
(1)求抛物线的解析式及顶点D的坐标;
(2)点P在抛物线的对称轴上,当△ACP的周长最小时,求出点P的坐标;
(3) 点N在抛物线上,点M在抛物线的对称轴上,是否存在以点N为直角顶点的Rt△DNM与Rt△BOC相似,若存在,请求出所有符合条件的点N的坐标;若不存在,请说明理由.
【答案】(1)![]() ,D(
,D(![]() ,
,![]() );(2)P(
);(2)P(![]() ,
,![]() );(3)存在.N(
);(3)存在.N(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
试题分析:(1)利用待定系数法求出抛物线解析式;
(2)确定出当△ACP的周长最小时,点P就是BC和对称轴的交点,利用两点间的距离公式计算即可;
(3)作出辅助线,利用tan∠MDN=2或![]() ,建立关于点N的横坐标的方程,求出即可.
,建立关于点N的横坐标的方程,求出即可.
试题解析:(1)由于抛物线![]() (a≠0)经过A(-1,0),B(2,0)两点,因此把A、B两点的坐标代入
(a≠0)经过A(-1,0),B(2,0)两点,因此把A、B两点的坐标代入![]() (a≠0),可得:
(a≠0),可得:![]() ;解方程组可得:
;解方程组可得: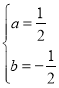 ,故抛物线的解析式为:
,故抛物线的解析式为:![]() ,∵
,∵![]() =
=![]() ,所以D的坐标为(
,所以D的坐标为(![]() ,
,![]() ).
).
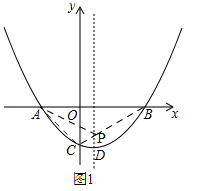
(2)如图1,设P(![]() ,k),∵
,k),∵![]() ,∴C(0,-1),∵A(-1,0),B(2,0),∴A、B两点关于对称轴对称,连接CB交对称轴于点P,则△ACP的周长最小.设直线BC为y=kx+b,则:
,∴C(0,-1),∵A(-1,0),B(2,0),∴A、B两点关于对称轴对称,连接CB交对称轴于点P,则△ACP的周长最小.设直线BC为y=kx+b,则:![]() ,解得:
,解得: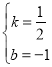 ,∴直线BC为:
,∴直线BC为:![]() .当x=
.当x=![]() 时,
时,![]() =
=![]() ,∴P(
,∴P(![]() ,
,![]() );
);
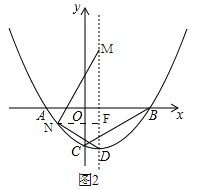
(3)存在.如图2,过点作NF⊥DM,∵B(2,0),C(0,﹣1),∴OB=2,OC=1,∴tan∠OBC=![]() ,tan∠OCB=
,tan∠OCB=![]() =2,设点N(m,
=2,设点N(m,![]() ),∴FN=|m﹣
),∴FN=|m﹣![]() |,FD=|
|,FD=|![]() |=|
|=|![]() |,∵Rt△DNM与Rt△BOC相似,∴∠MDN=∠OBC,或∠MDN=∠OCB;
|,∵Rt△DNM与Rt△BOC相似,∴∠MDN=∠OBC,或∠MDN=∠OCB;
①当∠MDN=∠OBC时,∴tan∠MDN=![]() =
=![]() ,∴
,∴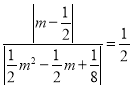 ,∴m=
,∴m=![]() (舍)或m=
(舍)或m=![]() 或m=
或m=![]() ,∴N(
,∴N(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
②当∠MDN=∠OCB时,∴tan∠MDN=![]() =2,∴
=2,∴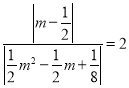 ,∴m=
,∴m=![]() (舍)或m=
(舍)或m=![]() 或m=
或m=![]() ,∴N(
,∴N(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
∴符合条件的点N的坐标(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某体育用品专卖店销售7个篮球和9个排球的总利润为355元,销售10个篮球和20个排球的总利润为650元.
(1)求每个篮球和每个排球的销售利润;
(2)已知每个篮球的进价为200元,每个排球的进价为160元,若该专卖店计划用不超过17400元购进篮球和排球共100个,且要求篮球数量不少于排球数量的一半,请你为专卖店设计符合要求的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上.则细线的另一端所在位置的点的坐标是 . 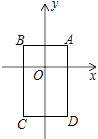
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四川汶川地震灾后重建中,某公司拟为灾区援建一所希望学校.公司经过调查了解:甲、乙两个工程队有能力承包建校工程,甲工程队单独完成建校工程的时间是乙工程队的1.5倍,甲、乙两队合作完成建校工程需要72天.
(1)甲、乙两队单独完成建校工程各需多少天?
(2)在施工过程中,该公司派一名技术人员在现场对施工质量进行全程监督,每天需要补助100元.若由甲工程队单独施工时平均每天的费用为0.8万元.现公司选择了乙工程队,要求其施工总费用不能超过甲工程队,则乙工程队单独施工时平均每天的费用最多为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】胜利中学会议室内的会议桌是一个长方形,长1.6米,宽1米,学校准备制作一块桌布,面积是桌面的2倍,且使桌面四周垂下的边等宽。若设四周垂下的边为x米,则应列得的方程为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=30°,D是AC边上的点;先将△ABC沿着BD翻折,翻折后△ABD的边AB交AC于点E;又将△BCE沿着BE翻折,C点恰好落在BD上,此时∠BEC=78°,则原三角形的∠ABC=度.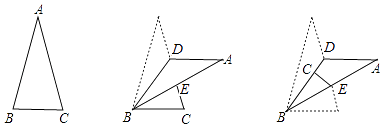
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( ) 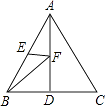
A.7.5
B.5
C.4
D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com