
���� ��1���������֪A��-2��0����C��4��0����-4��0������B��m��0������C��-4��0��ʱ��c=-4����y=0�õ�����x�ķ��̣�����һԪ���η��̸���ϵ���Ĺ�ϵ�����m=-4�������⣻����C��4��0��ʱ�����m=4��B��4��0���������ߵĽ���ʽΪy=-$\frac{1}{2}$��x+2����x-4����Ȼ�����ݵ�A��B��C������ɻ��������ߵĴ���ͼ��
��2������P��PD��x�ᣬ����ΪD��PD��BC���E�������BC�Ľ���ʽ�����P������Ϊ��x��-$\frac{1}{2}$x2+x+4������E��x��-x+4�������ݡ�CBP�����=$\frac{1}{2}$PE•OB�ɵõ������ε������x�ĺ�����ϵʽ����������䷽����⼴�ɣ�
��3�����������ߵĶԳ��᷽�̵õ������ߵĶԳ���Ϊx=1�����Q��1��y����Ȼ�����������ľ��빫ʽ�з�����⼴�ɣ�
��� �⣺��1����A��λ��y����࣬��OA=2��
��A��-2��0����
����������y���ཻ�ڵ�C��OC=4��
��C��4��0����-4��0����
��B��m��0����
��y=0�ã�-$\frac{1}{2}$x2+bx+c=0��
��C��-4��0��ʱ��c=-4����-$\frac{1}{2}$x2+bx-4=0��
��-2m=8�����m=-4��
��B��λ��A���Ҳ࣬
��m=-4����ȥ����
����C��4��0��ʱ��c=4����-$\frac{1}{2}$x2+bx+4=0��
��-2m=-8�����m=4��
��B��4��0����
�������ߵĽ���ʽΪy=-$\frac{1}{2}$��x+2����x-4������y=-$\frac{1}{2}$x2+x+4��
�����ߵĴ���ͼ����ͼ��ʾ��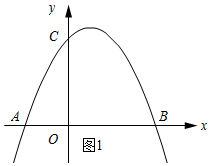
��2����ͼ2��ʾ������P��PD��x�ᣬ����ΪD��PD��BC���E��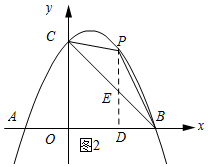
��BC�Ľ���ʽΪy=kx+4������B���������ã�4k+4=0�����k=-1��
��BC�Ľ���ʽΪy=-x+4��
���P��������x��-$\frac{1}{2}$x2+x+4������E��x��-x+4����
���CBP�����=$\frac{1}{2}$PE•OB=$\frac{1}{2}$��4����-$\frac{1}{2}$x2+2x��=-��x-2��2+4��
�൱x=2ʱ����CBP����������ֵ�����ֵΪ4��
��x=2���������ߵĽ���ʽ�ã�y=4��
���ʱ��P������Ϊ��2��4����
��3�������ߵĶԳ���Ϊx=-$\frac{b}{2a}$=1��
���Q��1��y����
��QA=QC��
���������ľ��빫ʽ��֪��$\sqrt{��1+2��^{2}+��y-0��^{2}}$=$\sqrt{��1-0��^{2}+��4-y��^{2}}$������ͬʱƽ���ã�9+y2=1+��4-y��2�������ã�8y=8�����y=1��
��Q��1��1����
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ������һ�κ��������κ����Ľ���ʽ���䷽������κ�������ֵ������ļ�ľ��빫ʽ�����������ǽ�����⣨1���Ĺؼ����г���CBP�������x�ĺ�����ϵʽ�ǽ�����⣨2���Ĺؼ������������ľ��빫ʽ�г�����y�ķ����ǽ�����⣨3���Ĺؼ���


 Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д� ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪һ�κ���y=x+3ͼ��x�ᡢy����A��B���㣬��P��һ�κ���y=x+3ͼ����λ�ڵ�һ������һ�㣬�Ե�PΪ�����������y=ax2+bx+c������B�������߽�x����C��D���㣨��ͼ����
��֪һ�κ���y=x+3ͼ��x�ᡢy����A��B���㣬��P��һ�κ���y=x+3ͼ����λ�ڵ�һ������һ�㣬�Ե�PΪ�����������y=ax2+bx+c������B�������߽�x����C��D���㣨��ͼ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��9��-2�� | B�� | ��-1��-2�� | C�� | ��9��2�� | D�� | ��-1��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
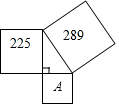 ��ͼ����ֱ�������ε�����Ϊ�������������Σ����ǵ��������Ϊ225��289��A����A��ֵΪ��������
��ͼ����ֱ�������ε�����Ϊ�������������Σ����ǵ��������Ϊ225��289��A����A��ֵΪ��������| A�� | 4 | B�� | 8 | C�� | 16 | D�� | 64 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com