
 小明将棱长为1厘米的正方体在课堂上堆成如图所示的形状,然后把露出来的面涂上不同的颜色,若按规律摆了3层,则被他涂上颜色的部分的面积为多少?四层呢?
小明将棱长为1厘米的正方体在课堂上堆成如图所示的形状,然后把露出来的面涂上不同的颜色,若按规律摆了3层,则被他涂上颜色的部分的面积为多少?四层呢? 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
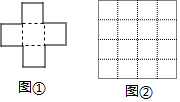 (1)一个无盖的正方体纸盒,沿某些棱剪开可以展成如图①所示的平面图形.你还能得到哪些不同的平面图形?请将它们表示出来(至少3种)
(1)一个无盖的正方体纸盒,沿某些棱剪开可以展成如图①所示的平面图形.你还能得到哪些不同的平面图形?请将它们表示出来(至少3种)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com