练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
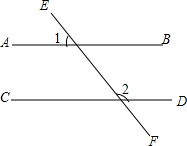
    19．如图，AB∥CD，∠1=48°，则∠2等于（　　）
    A．48°B．42°C．132°D．138°

    分析 由平行线的性质得出∠3=∠1=48°，再由邻补角关系即可得出∠2的度数．

    解答 解：如图所示：
    ∵AB∥CD，∠1=48°，
    ∴∠3=∠1=48°，
    ∴∠2=180°-∠3=132°．
    故选：C．

    点评 本题考查了平行线的性质、邻补角；熟练掌握平行线的性质，由平行线的性质得出同位角相等是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    9．要使分式$\frac{1}{3-x}$有意义，则（　　）
    A．x≠3B．x=3C．x＞3D．x＞-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．我市政府积极组织社区居民为希望工程捐款，为了解阳光社区居民捐款情况，对社区部分捐款户数进行分组统计（统计表如下），数据整理成如图所示的不完整统计图．已知A、B两组捐款户数直方图的高度比为1：5，请结合图中相关数据回答下列问题
    （1）A组捐款户数是多少？本次调查的样本容量是多少？
    （2）求出C组的频数并补全直方图；
    （3）若该社区有500户住户，请估计捐款不少于300元的户数是多少？
    组别捐款额（x）元
    A10≤x＜100
    B100≤x＜200
    C200≤x＜300
    D300≤x＜400
    Ex≥400

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．计算（-2）2012+（-2）2013的结果是（　　）
    A．22013B．-22012C．-22013D．-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．在同一平面内，已知∠AOB=60°，∠AOB=3∠AOC，则∠BOC=80°或40°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，△ABC为等边三角形，BF平分∠ABC，D是BF上的一点，连接AD，以AD为边在AD的左侧作等边△ADE，连接EB．
    （1）如图1，当E在BD上时，BE与ED的数量关系是BE=DE；
    （2）如图2，当E在直线BD外时，（1）的结论是否成立，说明理由；
    （3）当BD与BA满足什么条件时，以A，B，D，E为顶点的四边形为菱形，直接写出结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．如图，AB是⊙O的直径，AC是弦．OD⊥AC于D，OC与BD交于E，若BD=6，则DE等于（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

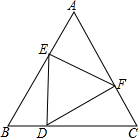    8．如图，△ABC是边长为9cm的等边三角形，D、E是边BC、BA上的动点，D点由B点开始以1cm/秒的速度向C点运动，E点由B点开始以2cm/秒的速度向A点运动，D、E同时出发．设运动时间为t，当其中一点到达边的端点时，运动便停止，在运动过程中始终保持∠EDF=60°．
    （1）求证：∠EDB=∠DFC；
    （2）当t=3秒时，判断△DEF的形状，并给出证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列根式是最简二次根式的是（　　）
    A．$\sqrt{0.5}$B．$\sqrt{{a}^{2}+{b}^{2}}$C．$\frac{1}{\sqrt{5}}$D．$\sqrt{50}$

    查看答案和解析>>

    同步练习册答案