
【题目】如图1,△ABC中,AB=AC,点D在BA的延长线上,点E在BC上,DE=DC,点F是DE与AC的交点,且DF=FE.
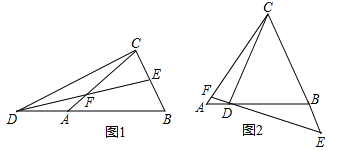
(1)图1中是否存在与∠BDE相等的角?若存在,请找出,并加以证明,若不存在,说明理由;
(2)求证:BE=EC;
(3)若将“点D在BA的延长线上,点E在BC上”和“点F是DE与AC的交点,且DF=FE”分别改为“点D在AB上,点E在CB的延长线上”和“点F是ED的延长线与AC的交点,且DF=kFE”,其他条件不变(如图2).当AB=1,∠ABC=a时,求BE的长(用含k、a的式子表示).
【答案】(1)∠DCA=∠BDE.(2)证明见解析;(3)![]() .
.
【解析】
试题(1)运用等腰三角形的性质及三角形的外角性质就可解决问题.
(2)过点E作EG∥AC,交AB于点G,如图1,要证BE=CE,只需证BG=AG,由DF=FE可证到DA=AG,只需证到DA=BG即DG=AB,也即DG=AC即可.只需证明△DCA≌△△EDG即可解决问题.
(3)过点A作AH⊥BC,垂足为H,如图2,可求出BC=2cosα.过点E作EG∥AC,交AB的延长线于点G,易证△DCA≌△△EDG,则有DA=EG,CA=DG=1.易证△ADF∽△GDE,则有![]() .由DF=kFE可得DE=EF-DF=(1-k)EF.从而可以求得AD=
.由DF=kFE可得DE=EF-DF=(1-k)EF.从而可以求得AD=![]() ,即GE=
,即GE=![]() ,易证△ABC∽△GBE,则有
,易证△ABC∽△GBE,则有![]() ,从而可以求出BE.
,从而可以求出BE.
试题解析:(1)∠DCA=∠BDE.
证明:∵AB=AC,DC=DE,
∴∠ABC=∠ACB,∠DEC=∠DCE.
∴∠BDE=∠DEC-∠DBC=∠DCE-∠ACB=∠DCA.
(2)过点E作EG∥AC,交AB于点G,如图1,
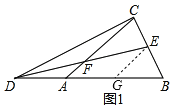
则有∠DAC=∠DGE.
在△DCA和△EDG中,
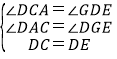
∴△DCA≌△EDG(AAS).
∴DA=EG,CA=DG.
∴DG=AB.
∴DA=BG.
∵AF∥EG,DF=EF,
∴DA=AG.
∴AG=BG.
∵EG∥AC,
∴BE=EC.
(3)过点E作EG∥AC,交AB的延长线于点G,如图2,

∵AB=AC,DC=DE,
∴∠ABC=∠ACB,∠DEC=∠DCE.
∴∠BDE=∠DBC-∠DEC=∠ACB-∠DCE=∠DCA.
∵AC∥EG,
∴∠DAC=∠DGE.
在△DCA和△EDG中,
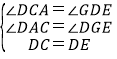
∴△DCA≌△EDG(AAS).
∴DA=EG,CA="DG"
∴DG=AB=1.
∵AF∥EG,
∴△ADF∽△GDE.
∴![]()
∵DF=kFE,
∴DE=EF-DF=(1-k)EF.
∴![]() .
.
∴AD=![]()
∴GE=AD=![]()
过点A作AH⊥BC,垂足为H,如图2,
∵AB="AC,AH⊥BC,"
∴BH="CH."
∴BC="2BH."
∵AB="1,∠ABC=α,"
∴BH=ABcos∠ABH="cosα."
∴BC="2cosα."
∵AC∥EG,
∴△ABC∽△GB.
∴![]() .
.
∴![]() .
.
∴BE=![]() .
.
∴BE的长为![]() .
.


科目:初中数学 来源: 题型:
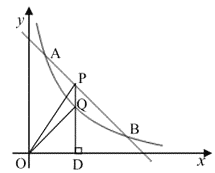
【题目】如图,一次函数y=kx+b与反比例函数![]() (x>0)的图象交于点A(a,3)和B(3,1).
(x>0)的图象交于点A(a,3)和B(3,1).
(1)求一次函数的解析式.
(2)观察图象,写出反比例函数值小于一次函数值时x的取值范围.
(3)点P是线段AB上一点,过点P作PD⊥x轴于点D,交反比例函数图象于点Q,连接OP、OQ,若△POQ的面积为![]() ,求P点的坐标。
,求P点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象分别与x轴、y轴交于点A、C,与反比列函数
的图象分别与x轴、y轴交于点A、C,与反比列函数![]() 的图象在第一象限内交于点P,过点P作
的图象在第一象限内交于点P,过点P作![]() 轴,垂足为B,且
轴,垂足为B,且![]() 的面积为9.
的面积为9.
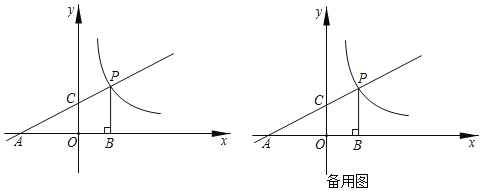
![]() 点A的坐标为______,点C的坐标为______,点P的坐标为______;
点A的坐标为______,点C的坐标为______,点P的坐标为______;
![]() 已知点Q在反比例函数
已知点Q在反比例函数![]() 的图象上,其横坐标为6,在x轴上确定一点M,使得
的图象上,其横坐标为6,在x轴上确定一点M,使得![]() 的周长最小,求出点M的坐标;
的周长最小,求出点M的坐标;
![]() 设点E是反比例函数
设点E是反比例函数![]() 在第一象限内图象上的一动点,且点E在直线PB的右侧,过点E作
在第一象限内图象上的一动点,且点E在直线PB的右侧,过点E作![]() 轴,垂足为F,当
轴,垂足为F,当![]() 和
和![]() 相似时,求动点E的坐标.
相似时,求动点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“佳佳商场”在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,“佳佳商场”应将这种商品的售价定为多少?
(2)物价局规定该商品的售价不能超过40元/件,“佳佳商场”为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=5 cm,BC=6 cm,点P从点A开始沿AB向终点B以1 cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2 cm/s的速度移动,如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动,设运动时间为t秒.
(1)填空:BQ=________,PB=________(用含t的代数式表示);
(2)当t为何值时,PQ的长度等于![]() cm?
cm?
(3)是否存在t的值,使得五边形APQCD的面积等于26 cm2?若存在,请求出此时t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆上一个动点(不与点A,B重合),D是弦AC上一点,过点D作DE⊥AB,垂足为E,过点C作半圆O的切线,交ED的延长线于点F.
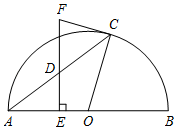
(1)求证:FC=FD.
(2)①当∠CAB的度数为 时,四边形OEFC是矩形;②若D是弦AC的中点,⊙O的半径为5,AC=8,则FC的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况,如图,通过直升机的镜头C观测到水平雪道一端A处的俯角为30°,另一端B处的俯角为45°.若直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则雪道AB的长度为( )

A.200 米B.(200+200![]() )米
)米
C.600 米D.(200+20![]() )米
)米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com