
分析 (1)根据幂的乘方、同底数幂的乘法即可解答本题;
(2)根据整式的乘法可以解答本题;
(3)根据幂的乘方和同底数幂的乘除法即可解答本题;
(4)根据负整数指数幂、零指数幂可以解答本题;
(5)根据同底数幂的乘法可以解答本题;
(6)根据积的乘方、同底数幂的乘法和合并同类项即可解答本题.
解答 解:(1)m•m3•(-m2)3
=m4•(-m6)
=-m10;
(2)(-0.25)2014×42015
=$(-\frac{1}{4})^{2014}×{4}^{2015}$
=4;
(3)2(a2)3-a2•a4+(2a4)2÷a2
=2a6-a6+4a8÷a2
=2a6-a6+4a6
=5a6;
(4)($\frac{1}{3}$)-3-(3.14-π)0+(-2)4
=27-1+16
=42;
(5)(p-q)4•(q-p)3•(p-q)2
=-(p-q)4•(p-q)3•(p-q)2
=(p-q)9;
(6)(-2x2)3+x2•x4-(-3x3)2
=(-8x6)+x6-9x6
=-16x6.
点评 本题考查整式的混合运算、零指数幂、负整数指数幂,解答本题的关键是明确它们各自的计算方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5.6万名考生 | B. | 2000名考生 | ||
| C. | 5.6万名考生的数学成绩 | D. | 2000名考生的数学成绩 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{50}$ | B. | $\sqrt{95}$ | C. | $\sqrt{15}$ | D. | $\sqrt{75}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
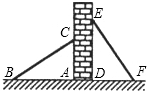 如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,且左边的滑梯与地面的夹角∠ABC=35°,则右边的滑梯与地面的夹角∠DFE=( )
如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,且左边的滑梯与地面的夹角∠ABC=35°,则右边的滑梯与地面的夹角∠DFE=( )| A. | 60° | B. | 55° | C. | 65° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com