
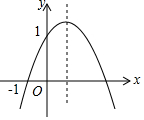 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,过点(0,1)和(-1,0),给出以下结论:①ab<0;②4a+c<1+b2;③0<c+b+a<2;④0<b<2;⑤当x>-1时,y>0;⑥8a+7b+2c-9<0其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,过点(0,1)和(-1,0),给出以下结论:①ab<0;②4a+c<1+b2;③0<c+b+a<2;④0<b<2;⑤当x>-1时,y>0;⑥8a+7b+2c-9<0其中正确结论的个数是( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
分析 由开口方向及对称轴位置可判断①;由c=1且抛物线与x轴有两个交点,即b2-4ac>0可得b2-4a>c-1,即可判断②;由抛物线过(-1,0)且c=1得a-b+c=0即b=a+1>0,继而可得-1<a<0即0<a+1<1,最后由a+b+c=a+a+1+1=2a+2=2(a+1)可判断③;由b=a+1且0<a+1<1可判断④;由函数图象知当x>-1时,图象有位于x轴上方也有位于x轴下方的,即可判断⑤;由8a+7b+2c-9=8a+7(a+1)+2-9=15a且a<0可判断⑥.
解答 解:∵开口向下且对称轴位于y轴右侧,
∴a<0,b>0,
∴ab<0,故①正确;
∵抛物线与x轴有两个交点且过点(0,1),
∴b2-4ac>0,c=1,
∴b2-4a>c-1,即4a+c<1+b2,故②正确;
∵抛物线过(-1,0),c=1,
∴a-b+c=0,
∴b=a+1>0,
∴-1<a<0,
∴0<a+1<1
又a+b+c=a+a+1+1=2a+2=2(a+1),且0<2(a+1)<2,
∴0<c+b+a<2,故③正确;
由③知,0<b=a+1<1,故④错误;
由函数图象知当x>-1时,y>0或y<0,故⑤错误;
∵8a+7b+2c-9=8a+7(a+1)+2-9=15a,且a<0,
∴8a+7b+2c-9<0,故⑥正确;
综上,正确的结论有①②③⑥共4个,
故选:C.
点评 本题主要考查二次函数图象与系数的关系,熟练将函数图象的开口方向、对称轴、顶点坐标、抛物线与坐标轴的交点及函数图象上特殊点的坐标转化成与系数有关的式子是解题的关键.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com