
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的对称轴为直线x=﹣1,下列结论正确的有_____(填序号).
①若图象过点(﹣3,y1)、(2,y2),则y1<y2;
②ac<0;
③2a﹣b=0;
④b2﹣4ac<0.
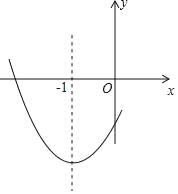
【答案】①②③
【解析】
①根据抛物线的对称轴找到(﹣3,y1)的对称点(1,y1),再与(2,y2)根据函数的增减性进行比较;②由抛物线的开口方向及与y轴的交点位置,即可得出a>0、c<0,进而可得出ac<0,结论②正确;③由-![]() =-1可得出2a-b=0,结论③正确;④由抛物线与x轴有两个交点,结合根的判别式可得出△=b2-4ac>0,结论④错误.综上即可得出结论.
=-1可得出2a-b=0,结论③正确;④由抛物线与x轴有两个交点,结合根的判别式可得出△=b2-4ac>0,结论④错误.综上即可得出结论.
解:①∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,
∴(﹣3,y1)的对称点是(1,y1),
∵抛物线的开口向上,
∴对称轴右侧y随x的增大而增大,
∴1<2,则y1<y2,
故①正确;
②∵抛物线的开口向上,
∴a>0,
∵抛物线与y轴交于y轴的负半轴,
∴c<0,
∴ac<0,
故②正确;
③∵抛物线的对称轴是x=-1,
∴-![]() =-1,
=-1,
∴b=2a,
∴2a-b=0,
故③正确;
④∵抛物线与x轴有两个交点,
∴△=b2-4ac>0,
故④错误.
故答案为:①②③.


科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且与反比例函数
,且与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
(1)分别求出一次函数与反比例函数的表达式;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,求四边形
,求四边形![]() 的面积
的面积![]() ;
;
(3)当![]() 时,
时,![]() 的取值范围是________.
的取值范围是________.
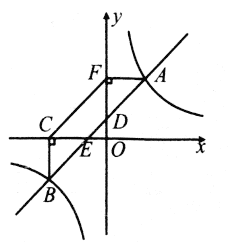
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援灾区,某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同.
(1)求A、B两种学习用品的单价各是多少元?
(2)若购买这批学习用品的费用不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面从认知、延伸、应用三个层面来研究一种几何模型.
(1)如图,已知点E是线段BC上一点,若∠AED=∠B=∠C.求证 △ABE∽△ECD.

(2)如图,已知点E、F是线段BC上两点,AE与DF交于点H,若∠AHD=∠B=∠C.
求证:△ABE∽△FCD.

(3)如图,⊙O是等边△ABC的外接圆,点D是![]() 上一点,连接BD并延长交AC的延长线于点E;连接CD并延长交AB的延长线于点F. 猜想BF、BC、CE三线段的关系,并说明理由.
上一点,连接BD并延长交AC的延长线于点E;连接CD并延长交AB的延长线于点F. 猜想BF、BC、CE三线段的关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A在x轴的正半轴上,顶点C的坐标为(1,![]() ).
).
(1)求图象过点B的反比例函数的解析式;
(2)求图象过点A,B的一次函数的解析式;
(3)在第一象限内,当以上所求一次函数的图象在所求反比例函数的图象下方时,请直接写出自变量x的取值范围.
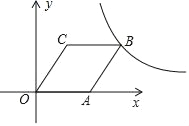
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润![]() 与投资量
与投资量![]() 成正比例关系,如图(1)所示;种植花卉的利润
成正比例关系,如图(1)所示;种植花卉的利润![]() 与投资量
与投资量![]() 成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)

(1)分别求出利润![]() 与
与![]() 关于投资量
关于投资量![]() 的函数关系式;
的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com