
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F.
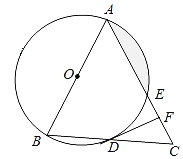
(1)求证:直线DF是⊙O的切线;
(2)求证:BC2=4CFAC;
(3)若⊙O的半径为2![]() ,∠CDF=15°,求阴影部分的面积.
,∠CDF=15°,求阴影部分的面积.
【答案】(1)见解析;(2)见解析;(3)4π﹣3![]()
【解析】
(1)如图所示,连接OD,证明∠CDF+∠ODB=90°,即可求解;
(2)证明△CFD∽△CDA,则CD2=CFAC,即BC2=4CFAC;
(3)S阴影部分=S扇形OAE﹣S△OAE即可求解.
解:(1)如图所示,连接OD,
∵AB=AC,
∴∠ABC=∠C,
∵OB=OD,
∴∠ODB=∠ABC=∠C,
∵DF⊥AC,
∴∠CDF+∠C=90°,
∴∠CDF+∠ODB=90°,
∴∠ODF=90°,
∴直线DF是⊙O的切线;
(2)连接AD,则AD⊥BC,则AB=AC,
则DB=DC=![]() BC,
BC,
∵∠CDF+∠C=90°,∠C+∠DAC=90°,
∴∠CDF=∠DAC,
∵∠DFC=∠ADC=90°,
∴△CFD∽△CDA,
∴CD2=CFAC,即BC2=4CFAC;
(3)连接OE,
∵∠CDF=15°,∠C=75°,
∴∠OAE=30°=∠OEA,
∴∠AOE=120°,
S△OAE=![]() AE×OEsin∠OEA=
AE×OEsin∠OEA=![]() ×2×2
×2×2![]() ×cos30°×2
×cos30°×2![]() ×sin30°=3
×sin30°=3![]() ,
,
S阴影部分=S扇形OAE﹣S△OAE=![]() ×π×(2
×π×(2![]() )2﹣3
)2﹣3![]() =4π﹣3
=4π﹣3![]() .
.


科目:初中数学 来源: 题型:
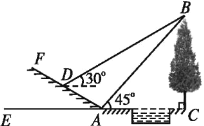
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是45°,若坡角∠FAE=30°,求大树的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
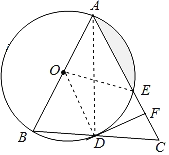
【题目】如图,已知AB是⊙O的直径,弦CD⊥AB于点H,过CD的延长线上一点E作⊙O的切线交AB的延长线于点F,切点为点G,连接AG交CD于点K.
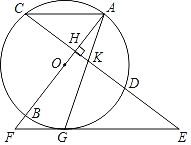
(1)求证:△EKG是等腰三角形;
(2)若KG2=KDGE,求证:AC∥EF;
(3)在(2)的条件下,若tanE=![]() ,AK=2
,AK=2![]() ,求FG的长.
,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
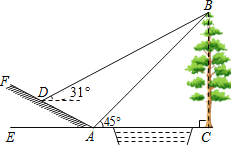
【题目】数学活动课上,小明和小红要测量小河对岸大树BC的高度,小红在点A测得大树顶端B的仰角为45°,小明从A点出发沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
(1)求小明从点A到点D的过程中,他上升的高度;
(2)依据他们测量的数据能否求出大树BC的高度?若能,请计算;若不能,请说明理由.(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AC=BC,∠ACB=120°,P为△ABC内部一点,且满足∠APB=∠BPC=150°.
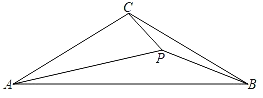
(1)求证:△PAB∽△PBC;
(2)求证:PA=3PC;
(3)若AB=10,求PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运输公司现将一批152吨的货物运往A,B两地,若用大小货车15辆,则恰好能一次性运完这批货.已知这两种大小货车的载货能力分别为12吨/辆和8吨/辆,其运往A,B两地的运费如下表所示:
目的地(车型) | A地(元/辆) | B地(元/辆) |
大货车 | 800 | 900 |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆.(用二元一次方程组解答)
(2)现安排其中的10辆货车前往A地,其余货车前往B地,设前往A地的大货车为x辆,前往A,B两地总费用为w元,试求w与x的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,延长CB至点M,使S△ABM=![]() ,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为________.
,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为________.
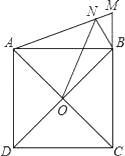
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把函数![]() 的图象绕点
的图象绕点![]() 旋转
旋转![]() ,得到新函数
,得到新函数![]() 的图象,我们称
的图象,我们称![]() 是
是![]() 关于点
关于点![]() 的相关函数.
的相关函数.![]() 的图象的对称轴与
的图象的对称轴与![]() 轴交点坐标为
轴交点坐标为![]() .
.
(1)填空:![]() 的值为 (用含
的值为 (用含![]() 的代数式表示)
的代数式表示)
(2)若![]() ,当
,当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,且
,且![]() ,求
,求![]() 的解析式;
的解析式;
(3)当![]() 时,
时,![]() 的图象与
的图象与![]() 轴相交于
轴相交于![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧).与
的右侧).与![]() 轴相交于点
轴相交于点![]() .把线段
.把线段![]() 原点
原点![]() 逆时针旋转
逆时针旋转![]() ,得到它的对应线段
,得到它的对应线段![]() ,若线
,若线![]() 与
与![]() 的图象有公共点,结合函数图象,求
的图象有公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料![]() ,乙种原料
,乙种原料![]() ,现用两种原料生产处
,现用两种原料生产处![]() 两种产品共
两种产品共![]() 件,已知生产每件
件,已知生产每件![]() 产品需甲种原料
产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,且每件
,且每件![]() 产品可获得
产品可获得![]() 元;生产每件
元;生产每件![]() 产品甲种原料
产品甲种原料![]() ,乙种原料
,乙种原料![]() ,且每件
,且每件![]() 产品可获利润
产品可获利润![]() 元,设生产
元,设生产![]() 产品
产品![]() 件(产品件数为整数件),根据以上信息解答下列问题:
件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产![]() 两种产品的方案有哪几种?
两种产品的方案有哪几种?
(2)设生产这![]() 件产品可获利
件产品可获利![]() 元,写出关于
元,写出关于![]() 的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com