
分析 列表得出所有等可能的情况数,找出两张卡片的数字都是非负数的情况,即可求出所求的概率.
解答 解:
列表如下:
| 1 | 2 | -2 | -3 | |
| 1 | --- | (2,1) | (-2,1) | (-3,1) |
| 2 | (1,3) | --- | (-2,2) | (-3,2) |
| -2 | (1,-2) | (2,-2) | --- | (-3,-2) |
| -3 | (1,-3) | (2,-3) | (-2,-3) | --- |
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比,正确区分是否是放回事件还是不放回事件是解题的关键.


科目:初中数学 来源: 题型:填空题
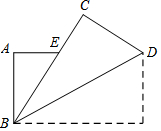 如图,把长方形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:
如图,把长方形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
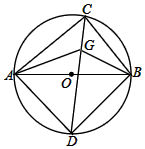 如图,AB为⊙O的直径,C为上半圆上一点,D为下半圆弧的中点,G为CD上一点,满足DA=DG
如图,AB为⊙O的直径,C为上半圆上一点,D为下半圆弧的中点,G为CD上一点,满足DA=DG查看答案和解析>>
科目:初中数学 来源: 题型:解答题
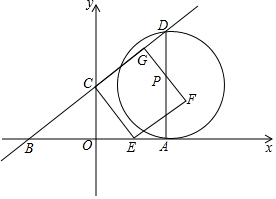 如图,在直角坐标系中,点A(12,0),点C在y轴正半轴上,点B在x轴的负半轴上,且$\frac{OC}{OB}$=$\frac{3}{4}$,过点C作CE⊥BC交x轴于点E,以CE为边在第一象限构造正方形CEFG,过点A作AD⊥x轴交直线BC于点D.记OC=3t,解答下列问题:
如图,在直角坐标系中,点A(12,0),点C在y轴正半轴上,点B在x轴的负半轴上,且$\frac{OC}{OB}$=$\frac{3}{4}$,过点C作CE⊥BC交x轴于点E,以CE为边在第一象限构造正方形CEFG,过点A作AD⊥x轴交直线BC于点D.记OC=3t,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (4) | B. | (3) | C. | (2) | D. | (1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,CB=CA,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
已知:如图,在△ABC中,CB=CA,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com