
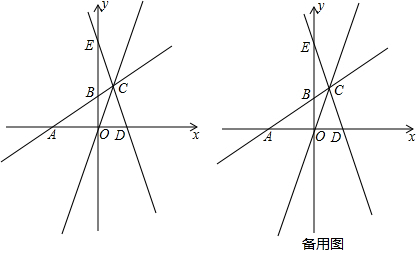
·ÖĪö £Ø1£©ĄūÓĆ·ĒøŗŠŌĒó³öOA£¬OB£¬½ų¶ųµĆ³öµćA£¬B×ų±ź£¬ÓĆ“ż¶ØĻµŹż·ØĒó³öÖ±ĻßAB½āĪöŹ½£¬ŌŁĮŖĮ¢Ö±ĻßOCµÄ½āĪöŹ½¼“æÉĒó³öµćCµÄ×ų±ź£»
£Ø2£©ĮŖĮ¢Ö±ĻßMNŗĶÖ±ĻßABµÄ½āĪöŹ½Ēó³öµćMµÄ×ų±ź£¬ĄūÓƶŌ³ĘĒó³öµćNµÄ×ų±ź£¬½ų¶ųĒó³öÖ±ĻßCEµÄ½āĪöŹ½¼“æÉ£»
£Ø3£©·ÖACĪŖ¾ŲŠĪµÄ±ßŗĶ¶Ō½ĒĻߣ¬ĄūÓĆ¾ŲŠĪµÄ¶Ō½ĒĻß»„ĻąĘ½·ÖĒŅĻąµČ£¬½čÖśÖŠµć×ų±ź¹«Ź½¼“æɽā¾ö£®
½ā“š ½ā£ŗ£Ø1£©”ß|OA-6|+$\sqrt{OB-\frac{9}{2}}$=0£¬
”ąOA=6£¬OB=$\frac{9}{2}$£¬
”ąA£Ø-6£¬0£©£¬B£Ø0£¬$\frac{9}{2}$£©£¬
”ą$\left\{\begin{array}{l}{-6k+b=0}\\{b=\frac{9}{2}}\end{array}\right.$£¬
”ą$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=\frac{9}{2}}\end{array}\right.$£¬
”ąÖ±ĻßABµÄ½āĪöŹ½ĪŖy=$\frac{3}{4}$x+$\frac{9}{2}$¢Ł£¬
”ßµćCŹĒÖ±ĻßABÓėOC£ŗy=3x¢ŚµÄ½»µć£¬
ĮŖĮ¢¢Ł¢Ś½āµĆ£¬$\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$£¬
”ąC£Ø2£¬6£©£»
£Ø2£©ČēĶ¼1£¬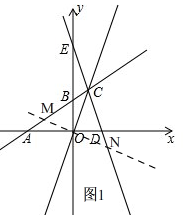
¹żµćO×÷Ö±ĻßMN”ĶOC½»Ö±ĻßABÓŚM£¬Ö±ĻßCEÓŚN£¬
”ßÖ±ĻßOCµÄ½āĪöŹ½ĪŖy=3x£¬
”ąÖ±ĻßMNµÄ½āĪöŹ½ĪŖy=-$\frac{1}{3}$x¢Ł£¬
”ßÖ±ĻßABµÄ½āĪöŹ½ĪŖy=$\frac{3}{4}$x+$\frac{9}{2}$¢Ś£¬
ĮŖĮ¢¢Ł¢Ś½āµĆ£¬x=-$\frac{54}{13}$£¬y=$\frac{18}{13}$£¬
”ąM£Ø-$\frac{54}{13}$£¬$\frac{18}{13}$£©£¬
ÓÉÕŪµžÖŖ£¬M£¬N¹ŲÓŚŌµć¶Ō³Ę£¬
”ąN£Ø$\frac{54}{13}$£¬-$\frac{18}{13}$£©£¬
”ßC£Ø2£¬6£©£¬
”ąÖ±ĻßCEµÄ½āĪöŹ½ĪŖy=-$\frac{24}{7}$x+$\frac{90}{7}$£¬
”ąE£Ø0£¬$\frac{90}{7}$£©£¬
”ąBE=$\frac{90}{7}$-$\frac{9}{2}$=$\frac{117}{14}$£¬
”ąS”÷BCE=$\frac{1}{2}$BE”Į|xC|=$\frac{1}{2}”Į\frac{117}{14}$”Į2=$\frac{117}{14}$£»
£Ø3£©ČēĶ¼2£¬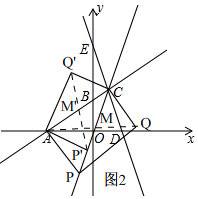
µ±ACĪŖ¾ŲŠĪµÄ±ßŹ±£¬AP”ĶAC£¬
”ßÖ±ĻßACµÄ½āĪöŹ½ĪŖy=$\frac{3}{4}$x+$\frac{9}{2}$£¬
”ąÖ±ĻßAPµÄ½āĪöŹ½ĪŖy=-$\frac{4}{3}$x-8¢Ł
”ßµćPŌŚÖ±Ļßy=3x¢ŚÉĻ£¬
ĮŖĮ¢¢Ł¢Ś½āµĆ£¬P£Ø-$\frac{24}{13}$£¬-$\frac{72}{13}$£©£¬
”ßC£Ø2£¬6£©
”ąPCµÄÖŠµćM£Ø$\frac{1}{13}$£¬$\frac{3}{13}$£©£¬
”ßĖıߊĪAPQCŹĒ¾ŲŠĪ£¬
”ąMŹĒAQµÄÖŠµć£¬
”ąQ£Ø$\frac{80}{13}$£¬$\frac{6}{13}$£©£»
µ±ACĪŖ¾ŲŠĪµÄ¶Ō½ĒĻߏ±£¬AP'”ĶOC£¬
”ßÖ±ĻßOCµÄ½āĪöŹ½ĪŖy=3x£¬
”ąÖ±ĻßAP'µÄ½āĪöŹ½ĪŖy=-$\frac{1}{3}$x-2¢Ū£¬
”ßµćP'ŌŚÖ±ĻßOCÉĻ£¬
”ąµćP'µÄ×ų±źĀś×ćy=3x¢Ü£¬ĮŖĮ¢¢Ū¢Ü½āµĆ£¬P'£Ø-$\frac{3}{5}$£¬-$\frac{9}{5}$£©£¬
”ßA£Ø-6£¬0£©£¬C£Ø2£¬6£©£¬
”ąACµÄÖŠµć×ų±źM'£Ø-2£¬3£©£¬
”ßĖıߊĪAP'CQ'ŹĒ¾ŲŠĪ£¬
”ąM'ŹĒP'Q'µÄÖŠµć£¬
”ąQ'£Ø-$\frac{17}{5}$£¬$\frac{39}{5}$£©£¬
¼“£ŗĀś×ćĢõ¼žµÄµćP£Ø-$\frac{24}{13}$£¬-$\frac{72}{13}$£©£¬Q£Ø$\frac{80}{13}$£¬$\frac{6}{13}$£©»ņP£Ø-$\frac{3}{5}$£¬-$\frac{9}{5}$£©£¬Q£Ø-$\frac{17}{5}$£¬$\frac{39}{5}$£©£®
µćĘĄ “ĖĢāŹĒŅ»“ĪŗÆŹż×ŪŗĻĢā£¬Ö÷ŅŖæ¼²éĮĖ·ĒøŗŠŌ£¬“ż¶ØĻµŹż·Ø£¬Čż½ĒŠĪµÄĆ껿¹«Ź½£¬¾ŲŠĪµÄŠŌÖŹ£¬ÕŪµžµÄŠŌÖŹ£¬½ā±¾ĢāµÄ¹Ų¼üŹĒĄūÓĆ“ż¶ØĻµŹż·ØĒóÖ±Ļß½āĪöŹ½£¬½ā£Ø3£©µÄ¹Ų¼üŹĒ·ÖĄąĢÖĀŪµÄĖ¼ĻėĖ¼æ¼ĪŹĢā£®


 Ńō¹āæĪĢĆæĪŹ±×÷ŅµĻµĮŠ“š°ø
Ńō¹āæĪĢĆæĪŹ±×÷ŅµĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ŅŃÖŖŌŚ¾ŲŠĪABCDÖŠ£¬AB=9£¬AD=6£¬µćEŌŚ±ßCDÉĻŅĘ¶Æ£¬ŃŲAE·ÕŪ¾ŲŠĪ£¬Ź¹µĆµćDĀäŌŚµćF“¦£¬ÄĒĆ“CFµÄ×īŠ”ÖµŹĒ3$\sqrt{13}$-6£®
ŅŃÖŖŌŚ¾ŲŠĪABCDÖŠ£¬AB=9£¬AD=6£¬µćEŌŚ±ßCDÉĻŅĘ¶Æ£¬ŃŲAE·ÕŪ¾ŲŠĪ£¬Ź¹µĆµćDĀäŌŚµćF“¦£¬ÄĒĆ“CFµÄ×īŠ”ÖµŹĒ3$\sqrt{13}$-6£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
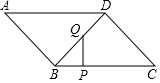 ČēĶ¼£¬ŌŚ?ABCDÖŠ£¬BC=20$\sqrt{2}$cm£¬CD=20cm£¬”ĻA=45”ć£¬¶ÆµćP“ÓµćB³ö·¢£¬ŃŲBCĻņµćCŌĖ¶Æ£¬¶ÆµćQ“ÓµćD³ö·¢£¬ŃŲDBĻņµćBŌĖ¶Æ£¬µćPŗĶµćQµÄŌĖ¶ÆĖŁ¶Č·Ö±šĪŖ3$\sqrt{2}$cm/sŗĶ2cm/s£¬Ņ»µćĶ£Ö¹ŌĖ¶Æ£¬ŌņĮķŅ»µćŅ²ĖęÖ®Ķ£Ö¹£¬µ±”÷BPQŹĒÖ±½ĒČż½ĒŠĪŹ±£¬ŠčŅŖ¾¹ż£Ø””””£©
ČēĶ¼£¬ŌŚ?ABCDÖŠ£¬BC=20$\sqrt{2}$cm£¬CD=20cm£¬”ĻA=45”ć£¬¶ÆµćP“ÓµćB³ö·¢£¬ŃŲBCĻņµćCŌĖ¶Æ£¬¶ÆµćQ“ÓµćD³ö·¢£¬ŃŲDBĻņµćBŌĖ¶Æ£¬µćPŗĶµćQµÄŌĖ¶ÆĖŁ¶Č·Ö±šĪŖ3$\sqrt{2}$cm/sŗĶ2cm/s£¬Ņ»µćĶ£Ö¹ŌĖ¶Æ£¬ŌņĮķŅ»µćŅ²ĖęÖ®Ķ£Ö¹£¬µ±”÷BPQŹĒÖ±½ĒČż½ĒŠĪŹ±£¬ŠčŅŖ¾¹ż£Ø””””£©| A£® | 4s | B£® | $\frac{5}{2}$s | C£® | $\frac{5}{2}$s»ņ4s | D£® | 6s |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
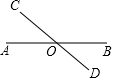 ČēĶ¼ĖłŹ¾£¬Ö±ĻßABŗĶCDĻą½»ÓŚµćO£¬Čō”ĻAODÓė”ĻBOCµÄŗĶĪŖ236”ć£¬Ōņ”ĻAOCµÄ¶ČŹżĪŖ62”ć£®
ČēĶ¼ĖłŹ¾£¬Ö±ĻßABŗĶCDĻą½»ÓŚµćO£¬Čō”ĻAODÓė”ĻBOCµÄŗĶĪŖ236”ć£¬Ōņ”ĻAOCµÄ¶ČŹżĪŖ62”ć£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | k£¼2£¬m£¾0 | B£® | k£¼2£¬m£¼0 | C£® | k£¾2£¬m£¾0 | D£® | k£¾2£¬m£¼0 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 1£¬1£¬$\sqrt{2}$ | B£® | 2£¬3£¬4 | C£® | 4£¬5£¬6 | D£® | 6£¬8£¬11 |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com