

���� ��1����CG��OA��G��BH��OA��H����A��14��0����B��11��4����C��3��4���������AH=3��BC=8��OG=3��CG=BH=4����CB��OA����t=4ʱ��OE=8�����Եõ�BC=OE���Ӷ����Եó����ۣ�
��2����ͼ2����֪�������ı���COEF��ֱ������ʱ��EF=GE������3t-5=2t-3���Ӷ��������t��ֵ��
��3��ͨ�����㣬����֪��Ҫʹ�ı���COEF�����Σ�����3t=10��2t=5�����tֵ����ȣ��ʲ��������Σ�
��� 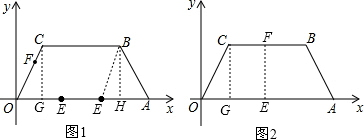 �⣺��1����ͼ1����CG��OA��G��BH��OA��H����B��11��4����C��3��4����
�⣺��1����ͼ1����CG��OA��G��BH��OA��H����B��11��4����C��3��4����
���CGO=��BHA=90�㣬OG=3��CG=4��AH=3��BH=4��BC=8��
���CGO�ա�BHA��
��OC=AB��
��Rt��OGC���ɹ��ɶ�������OC2=OG2+CG2��
��OC2=32+42��
��OC=5��
��AB=5��
�ߵ�E��ÿ��2����λ���ٶȴ�O�����������OA��A���˶���
�൱�˶�ʱ��Ϊ4ʱ��OE=8��
��OE=BC��
��BC��OA��
���ı���COEB��ƽ���ı��Σ�
��2����ͼ2����t��ʱEF��OA��
��OC+CF=3t��OE=2t��CF=GE��
��3t-OC=2t-OG��
��3t-5=2t-3��
��ã�t=2��
��3�������˶�t����ı���COEF�����Σ�
��CF=OE=CO=5��
��OC+CF=3t=10��0E=2t=5��
��t=$\frac{10}{3}$����t=$\frac{5}{2}$��
��$\frac{10}{3}$��$\frac{5}{2}$��
����ڷ���������t��
���� ���⿼���˵������ε��ж������ʣ����ε��ж������ʣ�ֱ�����ε����ʣ����ɶ��������ã�������������ã������ڶ�������ʱ��һ��Ҫע��δ֪����ȡֵ��Χ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
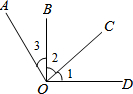 ��ͼ��ʾ����֪��AOC=��BOD=90�㣬��1=30�㣮
��ͼ��ʾ����֪��AOC=��BOD=90�㣬��1=30�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
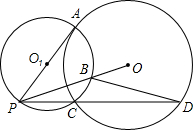 ��ͼ��P�ǡ�O��һ�㣬PA�С�O�ڵ�A��PAΪֱ������O1����PO�ڵ�B������O�ڵ�C������PC���ӳ�����O�ڵ�D������BD��
��ͼ��P�ǡ�O��һ�㣬PA�С�O�ڵ�A��PAΪֱ������O1����PO�ڵ�B������O�ڵ�C������PC���ӳ�����O�ڵ�D������BD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
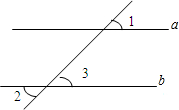 ��ϸ��һ�룬����������������
��ϸ��һ�룬�����������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
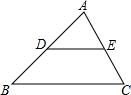 ��ͼ��ʾ���ڡ�ABC�У���D��E�ֱ��DZ�AB��AC���е㣬���ADE�͡�ABC���ܳ�֮�ȵ��ڣ�������
��ͼ��ʾ���ڡ�ABC�У���D��E�ֱ��DZ�AB��AC���е㣬���ADE�͡�ABC���ܳ�֮�ȵ��ڣ�������| A�� | $\frac{1}{4}$ | B�� | 4 | C�� | $\frac{1}{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com