
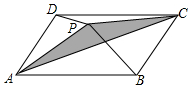
 如上右图,已知P是平行四边形ABCD内一点,且S△PAB=7,S△PAD=4,则阴影部分的面积是3.
如上右图,已知P是平行四边形ABCD内一点,且S△PAB=7,S△PAD=4,则阴影部分的面积是3.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
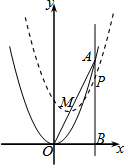 如图,直线x=2上有一点A(2,4),将抛物线y=x2的顶点在线段OA上移动到M,得到
如图,直线x=2上有一点A(2,4),将抛物线y=x2的顶点在线段OA上移动到M,得到查看答案和解析>>
科目:初中数学 来源: 题型:解答题
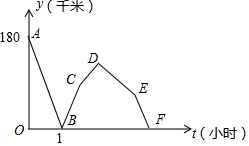 一辆轿车从甲城驶往乙城,同时一辆卡车从乙城驶往甲城,两车沿相同路线匀速行驶,轿车到达乙城停留一段时间后,按原路原速返回甲城;卡车到达甲城比轿车返回甲城早0.5小时,轿车比卡车每小时多行驶60千米,两车到达甲城后均停止行驶,两车之间的路程y(千米)与轿车行驶时间t(小时)的函数图象如图所示,请结合图象提供的信息解答下列问题:
一辆轿车从甲城驶往乙城,同时一辆卡车从乙城驶往甲城,两车沿相同路线匀速行驶,轿车到达乙城停留一段时间后,按原路原速返回甲城;卡车到达甲城比轿车返回甲城早0.5小时,轿车比卡车每小时多行驶60千米,两车到达甲城后均停止行驶,两车之间的路程y(千米)与轿车行驶时间t(小时)的函数图象如图所示,请结合图象提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
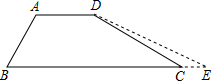 为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=12$\sqrt{3}$米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE=$\frac{3}{13}$$\sqrt{3}$,则CE的长为8米.
为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=12$\sqrt{3}$米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE=$\frac{3}{13}$$\sqrt{3}$,则CE的长为8米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<-2 | B. | x≤-1 | C. | x≤1 | D. | x<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≤-1 | B. | m<-1 | C. | -1<m≤0 | D. | -1≤m<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com