
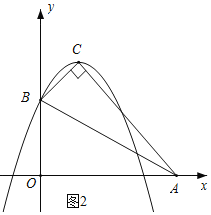
【题目】如图,已知在平面直角坐标系xOy中,点A(4,0)是抛物线y=ax2+2x-c上的一点,将此抛物线向下平移6个单位后经过点B(0,2),平移后所得的新抛物线的顶点记为C,新抛物线的对称轴与线段AB的交点记为P.
(1)求平移后所得到的新抛物线的表达式,并写出点C的坐标;
(2)求∠CAB的正切值;
(3)如果点Q是新抛物线对称轴上的一点,且△BCQ与△ACP相似,求点Q的坐标.

【答案】(1)y=-x2+2x+2,点C的坐标为(1,3);(2)tan∠CAB=![]() ;(3)Q(1,
;(3)Q(1,![]() ).
).
【解析】
(1)先根据点B(0,2)向上平移6个单位得到点B'(0,8),将A(4,0),B'(0,8)分别代入y=ax2+2x-c,得原抛物线为y=-x2+2x+8,向下平移6个单位后所得的新抛物线为y=-x2+2x+2,据此求得顶点C的坐标;
(2)根据A(4,0),B(0,2),C(1,3),得到AB2=20,AC2=18,BC2=2,进而得出AB2=AC2+BC2,根据∠ACB=90°,求得tan∠CAB的值即可;
(3)先设抛物线的对称轴x=1与x轴交于点H,根据![]() =
=![]() ,求得PH=
,求得PH=![]() AH=
AH=![]() ,进而得到P(1,
,进而得到P(1,![]() ),再由HA=HC=3,得∠HCA=45°,根据当点Q在点C下方时,∠BCQ=∠ACP,因此△BCQ与△ACP相似分两种情况,根据相似三角形的性质即可得到点Q的坐标.
),再由HA=HC=3,得∠HCA=45°,根据当点Q在点C下方时,∠BCQ=∠ACP,因此△BCQ与△ACP相似分两种情况,根据相似三角形的性质即可得到点Q的坐标.
解:(1)点B(0,2)向上平移6个单位得到点B'(0,8),
将A(4,0),B'(0,8)分别代入y=ax2+2x-c,得
![]() ,
,
解得![]() ,
,
∴原抛物线为y=-x2+2x+8,向下平移6个单位后所得的新抛物线为y=-x2+2x+2,
∴顶点C的坐标为(1,3);
(2)如图2,由A(4,0),B(0,2),C(1,3),得
AB2=20,AC2=18,BC2=2,
∴AB2=AC2+BC2,
∴∠ACB=90°,
∴tan∠CAB=![]() =
=![]() =
=![]() ;
;
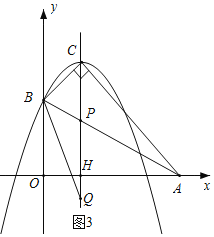
(3)如图3,设抛物线的对称轴x=1与x轴交于点H,
由![]() =
=![]() =
=![]() ,得PH=
,得PH=![]() AH=
AH=![]() ,
,
∴P(1,![]() ),
),
由HA=HC=3,得∠HCA=45°,
∴当点Q在点C下方时,∠BCQ=∠ACP,
因此△BCQ与△ACP相似分两种情况:
①如图3,当![]() =
=![]() 时,
时,![]() =
=![]() ,
,
解得CQ=4,
此时Q(1,-1);
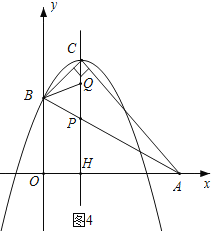
②如图4,当![]() =
=![]() 时,
时,![]() =
=![]() ,
,
解得CQ=![]() ,
,
此时Q(1,![]() ).
).


科目:初中数学 来源: 题型:
【题目】“创科集团”会议室内的一个长为6米、宽为4米的矩形ABCD墙面需要进行装饰,设计图案如图所示,将矩形ABCD墙面分割成3个区域,中间“十”字形区域甲的宽度均为1米,四个角为四个全等的直角三角形,△AEF,△BGH,△CMN,△DPQ为区域乙,剩下部分为区域丙,其中AE=BG=CN=DP,设EG=HM=NP=FQ=x(米)(1≤x≤3)
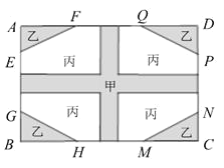
(1)当x=2时,求区域乙的面积;
(2)求区域丙的面积的最大值;
(3)为了图案富有美感,设置区域乙与区域丙的面积之比为1:4,在区域甲、区域乙、区域丙分别嵌贴甲、乙、丙三种不同的装饰板,这三种装饰板每平方米的单价分别为a(百元),b(百元),c(百元)(a,b,c均为整数,且6<a<10),若a+b+c=20,整个墙面嵌贴共花费了150(百元),求三种装饰板每平方米的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() 长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
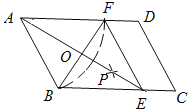
(1)四边形ABEF是_______;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为________,∠ABC=________°.(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
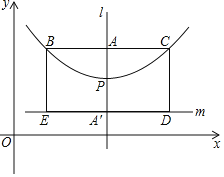
【题目】如图,在顶点为P的抛物线y=a(x-h)2+k(a≠0)的对称轴1的直线上取点A(h,k+![]() ),过A作BC⊥l交抛物线于B、C两点(B在C的左侧),点和点A关于点P对称,过A作直线m⊥l.又分别过点B,C作直线BE⊥m和CD⊥m,垂足为E,D.在这里,我们把点A叫此抛物线的焦点,BC叫此抛物线的直径,矩形BCDE叫此抛物线的焦点矩形.
),过A作BC⊥l交抛物线于B、C两点(B在C的左侧),点和点A关于点P对称,过A作直线m⊥l.又分别过点B,C作直线BE⊥m和CD⊥m,垂足为E,D.在这里,我们把点A叫此抛物线的焦点,BC叫此抛物线的直径,矩形BCDE叫此抛物线的焦点矩形.
(1)直接写出抛物线y=![]() x2的焦点坐标以及直径的长.
x2的焦点坐标以及直径的长.
(2)求抛物线y=![]() x2-
x2-![]() x+
x+![]() 的焦点坐标以及直径的长.
的焦点坐标以及直径的长.
(3)已知抛物线y=a(x-h)2+k(a≠0)的直径为![]() ,求a的值.
,求a的值.
(4)①已知抛物线y=a(x-h)2+k(a≠0)的焦点矩形的面积为2,求a的值.
②直接写出抛物线y=![]() x2-
x2-![]() x+
x+![]() 的焦点短形与抛物线y=x2-2mx+m2+1公共点个数分别是1个以及2个时m的值.
的焦点短形与抛物线y=x2-2mx+m2+1公共点个数分别是1个以及2个时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1相交于点O.以点O为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的直角坐标系.以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在x轴的正半轴上得到点A1,A2,A3,…,An,则点An的坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
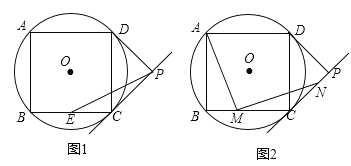
【题目】如图,四边形ABCD是⊙O的内接正方形,AB=4,PC、PD是⊙O的两条切线,C、D为切点.
(1)如图1,求⊙O的半径;
(2)如图1,若点E是BC的中点,连接PE,求PE的长度;
(3)如图2,若点M是BC边上任意一点(不含B、C),以点M为直角顶点,在BC的上方作∠AMN=90°,交直线CP于点N,求证:AM=MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知y是x(x>0)的函数,表1中给出了几组x与y的对应值:
表1:
x | … |
| 1 |
| 2 |
| 3 | … |
y | … | 6 | 3 | 2 |
|
| 1 | … |
⑴以表中各对对应值为坐标,在图1的直角坐标系中描出各点,用光滑曲线顺次连接.由图像知,它是我们已经学过的哪类函数?求出函数解析式,并直接写出![]() 的值;
的值;
⑵如果一次函数图像与⑴中图像交于(1,3)和(3,1)两点,在第一、四象限内当x在什么范围时,一次函数的值小于⑴中函数的值?请直接写出答案.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com