
【题目】如图,P是正△ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB. 
(1)求旋转角的度数;
(2)求点P与点P′之间的距离;
(3)求∠APB的度数.
【答案】
(1)解:由∠BAC=60°可知旋转角的度数为60°
(2)解:连接PP′,由题意可知AP′=AP=6,
∵旋转角的度数为60°,
∴∠PAP′=60°.
∴△APP′为等边三角形,
∴PP′=AP=AP′=6
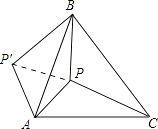
(3)解:∵BP′=PC=10,BP=8,PP′=6,
∴PP′2+BP2=BP′2,
∴△BPP′为直角三角形,且∠BPP′=90°
∴∠APB=∠BPP′+∠APP′=90°+60°=150°
【解析】(1)由∠BAC=60°可知旋转角的度数为60°;(2)由已知△PAC绕点A逆时针旋转后,得到△P′AB,可得△PAC≌△P′AB,PA=P′A,旋转角∠P′AP=∠BAC=60°,所以△APP′为等边三角形,即可求得PP′;(3)由△APP′为等边三角形,得∠APP′=60°,在△PP′B中,已知三边,用勾股定理逆定理证出直角三角形,得出∠P′PB=90°,可求∠APB的度数.


科目:初中数学 来源: 题型:
【题目】某运输队要运300 t物资到江边防洪.
(1)运输时间t(单位:h)与运输速度v(单位:t/h)之间有怎样的函数关系式?
(2)运了一半时,接到防洪指挥部命令,剩下的物资要在2 h之内运到江边,则运输速度至少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组从![]() 地出发,在南北方向的路上检修线路,如果规定向北行驶为正,向南行驶为负,一天行驶记录如下:(单位:千米)
地出发,在南北方向的路上检修线路,如果规定向北行驶为正,向南行驶为负,一天行驶记录如下:(单位:千米)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
通过列式计算:
![]() 收工时检修工人离
收工时检修工人离![]() 地多远?在
地多远?在![]() 地的哪个方向上?
地的哪个方向上?
![]() 若检修人员用的是耗油为每千米
若检修人员用的是耗油为每千米![]() 升的汽车作交通工具,那么这天中,这辆汽车共耗油多少升?
升的汽车作交通工具,那么这天中,这辆汽车共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料一:一个正整数x能写成x=a2﹣b2(a,b均为正整数,且a≠b),则称x为“雪松数”,a,b为x的一个平方差分解,在x的所有平方差分解中,若a2+b2最大,则称a,b为x的最佳平方差分解,此时F(x)=a2+b2.
例如:24=72﹣52,24为雪松数,7和5为24的一个平方差分解,32=92﹣72,32=62﹣22,因为92+72>62+22,所以9和7为32的最佳平方差分解,F(32)=92+72
材料二:若一个四位正整数,它的千位数字与个位数字相同,百位数字与十位数字相同,但四个数字不全相同,则称这个四位数为“南麓数”.例如4334,5665均为“南麓数”.
根据材料回答:
(1)请直接写出两个雪松数,并分别写出它们的一对平方差分解;
(2)试证明10不是雪松数;
(3)若一个数t既是“雪松数”又是“南麓数”,并且另一个“南麓数”的前两位数字组成的两位数与后两位数字组成的两位数恰好是t的一个平方差分解,请求出所有满足条件的数t中F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】百货商店服装专柜在销售中发现:某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.为占有市场份额,在确保盈利的前提下.
(1)降价多少元时,每星期盈利为6125元.
(2)降价多少元时,每星期盈利额最大,最大盈利额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD.
(1)求证:EG=FG.
(2)若将△DEC的边EC沿AC方向移动,变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
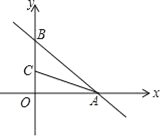
【题目】在平面直角坐标系中,已知一次函数y=﹣![]() x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
A. (0,3) B. (0,![]() ) C. (0,
) C. (0,![]() ) D. (0,
) D. (0,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三一班五个劳动竞赛小组一天植树的棵数是:10,10,12,x,8,如果这组数据的众数与平均数相等,那么这组数据的中位数是( )
A. 12 B. 10 C. 9 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com