
分析 (1)设甲种球拍的单价为x元,乙种球拍的单价为(x-40)元,根据题意列方程即可得到结论;
(2)设购买m副甲种球拍总费用最低,总费用为y元,根据题意列不等式得到m≥$\frac{200}{3}$,根据函数的性质即可得到结论.
解答 解:(1)设甲种球拍的单价为x元,乙种球拍的单价为(x-40)元,
根据题意得,4x=6(x-40),
解得:x=120,
x-40=80,
答:甲种球拍的单价为120元,乙种球拍的单价80元;
(2)设购买m副甲种球拍总费用最低,总费用为y元,
根据题意得,120m≥3×80(100-m),
解得:m≥$\frac{200}{3}$,
∵y=120m+80(100-m)=40m+8000
∵40>0,
∴当m取最小值时,总费用为y最小,
∴m=67时,总费用为y最小,
答:购买67副甲种球拍总费用最低.
点评 本题考查了一次函数的应用,一元一次不等式的应用,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:解答题
 有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,A、B两点之间的距离是70米.甲、乙两机器人分别从A、B两点同时同向出发,乙机器人始终以60米/分的速度行走,乙行走7分钟到达C点.设两机器人出发时间为t(分钟),当t=2分钟时,甲追上乙.前3分钟甲机器人的速度保持不变,3分钟后甲的速度变为另一数值.已知在3≤t≤4分钟时,甲、乙两机器人之间的距离保持不变.
有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,A、B两点之间的距离是70米.甲、乙两机器人分别从A、B两点同时同向出发,乙机器人始终以60米/分的速度行走,乙行走7分钟到达C点.设两机器人出发时间为t(分钟),当t=2分钟时,甲追上乙.前3分钟甲机器人的速度保持不变,3分钟后甲的速度变为另一数值.已知在3≤t≤4分钟时,甲、乙两机器人之间的距离保持不变.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 亏损8元 | B. | 赚了12元 | C. | 亏损了12元 | D. | 不亏不损 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
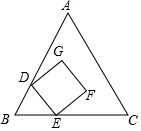 如图为等边三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB,BC上,且BD=BE,若AC=19,GF=6,则点F到AC的距离为$\frac{13}{2}$$\sqrt{3}$-6.
如图为等边三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB,BC上,且BD=BE,若AC=19,GF=6,则点F到AC的距离为$\frac{13}{2}$$\sqrt{3}$-6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com