
如图,已知四边形ABCD的对角线AC与BD相交于点O,且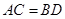 ,
,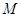 、
、 分别是
分别是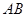 、
、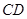 的中点,
的中点,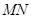 分别交
分别交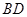 、
、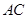 于点
于点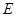 、
、 .你能说出
.你能说出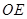 与
与 的大小关系并加以证明吗?
的大小关系并加以证明吗?
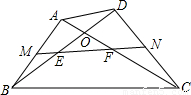

【解析】
试题分析:取AD的中点G,连接MG,NG,构造三角形的中位线,根据三角形的中位线定理及平行线的性质即可证得结果。
如图,取AD的中点G,连接MG,NG,

∵G、N分别为AD、CD的中点,
∴GN是△ACD的中位线,
∴GN= AC,
AC,
同理可得,GM= BD,
BD,
∵AC=BD,
∴GN=GM,
∴∠GMN=∠GNM,
又∵MG∥OE,NG∥OF,
∴∠OEF=∠GMN=∠GNM=∠OFE,
∴OE=OF.
考点:本题考查了三角形的中位线定理,平行线的性质
点评:解答本题的关键是注意此题中的辅助线:构造三角形的中位线.运用三角形的中位线的数量关系和位置关系进行分析证明.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
 |
| BDC |
 的延长线分别交于点F、E,且
的延长线分别交于点F、E,且 |
| BF |
 |
| AD |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com