Question

已知：抛物线y=x²+mx+n与x轴交A、B两点（A点在B点左侧），B（3，0），且经过C（2，-3），与y轴交于点D，
（1）求此抛物线的解析式及顶点F的坐标；
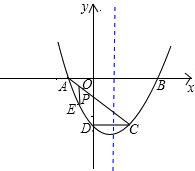
（2）P是线段AC上的一个动点，过P点作y轴的平行线交抛物于E点，求线段PE长度的最大值；
（3）在（1）的条件下，在x轴上是否存在两个点G、H（G在H的左侧），且GH=2，使得线段GF+FC+CH+HG的长度和为最小？如果存在，求出G、H的坐标；如果不存在，说明理由．

Answer 1

分析：（1）分别把B（3，0），C（2，-3）两点的坐标代入y=x²+mx+n中即可确定此抛物线的解析式，然后就可以确定顶点F的坐标；
（2）本题需先根据（1）中的函数关系式得出A与D的坐标，再设出直线AC的解析式为y=kx+b，解出k、b的值，从而得出直线AC的解析式，再设P的横坐标为x，即纵坐标为-x-1，得出PE的解析式来，最后即可求出线段PE长度的最大值．
（3）本题需先根据已知条件，设出点H和点G的坐标，再用x表示出GF²+CH²的值，即可得出线段GF+CH的长度和最小时x的值，从而求出G、H的坐标．

解答：解：（1）∵抛物线y=x²+mx+n与x轴交A、B两点（A点在B点左侧），B（3，0），且经过C（2，-3），
∴

0=9+3m+n -3=4+2m+n

，
解之得m=-2，n=-3，
∴抛物线的解析式为y=x²-2x-3，
∴y=x²-2x-3=y=x²-2x+1-4=（x-1）²-4，
∴F的坐标为（1，-4）；

（2）如图，∵y=x²-2x-3=y=x²-2x+1-4=（x-1）²-4，
∴当y=0时，x=3或x=-1，对称轴为x=1，
当x=0时，y=-3，
∴A（-1，0），D（0，-3），
设直线AC的解析式为y=kx+b，
依题意得

0=-k+b -3=2k+b

，
解之得k=-1，b=-1，
∴直线AC的解析式为y=-x-1，
设P的横坐标为x，那么纵坐标为-x-1，
∵EP∥OD，
∴E的横坐标为x，纵坐标为，
∵P是线段AC上的一个动点，
∴PE=-（x²-2x-3+x+1）=-x²+x+2，
∴当x=

1

2

时，PE的长度最大，线段PE长度的最大值为

4×(-1)×2-1

-4

=

9

4

；

（3）∵GH=2，CF=

(2-1)2+[-3-(-4)]2

=

2

∴GH、CF的长是定值．
∴使得线段GF+FC+CH+HG的长度和为最小，
则线段GF+CH的长度和最小．
∵设点H的坐标为（x，0），则点G的坐标为（x-2，0），
则GF²+CH²=[1-（x-2）]²+4²+（2-x）²+3²
=2x²-10x+38
∴当x=-

11

4

时，线段GF+CH的长度和最小．
G、H的坐标分别是（-

19

4

，0）（-

11

4

，0）．

点评：本题考查的是二次函数的综合题型，其中涉及的知识点有抛物线的平移、抛物线交点坐标与其解析式的组成的方程组的解的关系及等腰三角形的性质与判定，也利用了三角函数的定义，综合性比较强，定义学生的能力要求比较高，平时加强训练．