
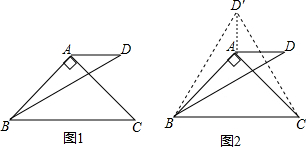
分析 (1)作辅助线构建全等三角形,证明△ABD≌△ABD′得△BD′C是等边三角形,再证明△AD′B≌△AD′C得∠AD′B=$\frac{1}{2}$∠BD′C=30°,则∠ADB=∠AD′B=30°;
(2)分两种情况进行讨论:第一种情况:当60°<α≤120°时,利用全等先求∠ABC和∠ABD的度数,从而得∠ABD′和∠D′BC的度数,得到△BD′C是等边三角形,根据(1)同理得出∠ADB=∠AD′B=30°;第二种情况:当0°<α<60°时,仍然按此过程求出∠ADB=∠AD′B=150°;
(3)分三种情况讨论:第一种情况:如图4,当120°<α<180°时,构建等边三角形D′BC,可知此时满足α-β=120°时,∠ADB的度数与(1)相同为30°;第二种情况:如图5,当0°<α<120°时,当△BDC是等边三角形时,即满足β=60°时,∠ADB的度数与(1)相同为30°;第三种情况:如图6,当120°<α<180°时,构建等边三角形DBC,与第二种情况一样,即满足β=60°时,∠ADB的度数与(1)相同为30°.
解答 解:(1)如图1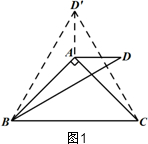
作∠AB D′=∠ABD,B D′=BD,连接CD′,AD′,
∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∵∠DBC=30°,
∴∠ABD=∠ABC-∠DBC=15°,
∵AB=AB,∠AB D′=∠ABD,B D′=BD,
∴△ABD≌△ABD′,
∴∠ABD=∠ABD′=15°,∠ADB=∠AD′B,
∴∠D′BC=∠ABD′+∠ABC=60°,
∵BD=BD′,BD=BC,
∴BD′=BC,
∴△D′BC是等边三角形,
∴D′B=D′C,∠BD′C=60°,
∵AB=AC,AD'=AD',
∴△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∴∠AD′B=$\frac{1}{2}$∠BD′C=30°,
∴∠ADB=30°,
(2)解:第一种情况:当60°<α≤120°时,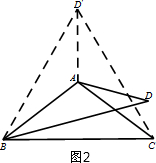
如图2,作∠AB D′=∠ABD,B D′=BD,连接CD′,AD′,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=α,
∴∠ABC=$\frac{180°-α}{2}$=90°-$\frac{α}{2}$,
∴∠ABD=∠ABC-∠DBC=90°-$\frac{α}{2}$-β,
同(1)可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=90°-$\frac{α}{2}$-β,BD=BD′,∠ADB=∠AD′B
∴∠D′BC=∠ABD′+∠ABC=90°-$\frac{α}{2}-β+90°-\frac{α}{2}$=180°-(α+β),
∵α+β=120°,
∴∠D′BC=60°,
以下同(1)可求得∠ADB=30°,
第二种情况:当0°<α<60°时,
如图3,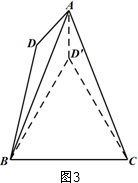
作∠AB D′=∠ABD,B D′=BD,连接CD′,AD′.同理可得:∠ABC=$\frac{180°-α}{2}=90°-\frac{α}{2}$,
∴∠ABD=∠DBC-∠ABC=$β-(90°-\frac{α}{2})$,
同(1)可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=$β-(90°-\frac{α}{2})$,BD=BD′,∠ADB=∠AD′B,
∴∠D′BC=∠ABC-∠ABD′=90°-$\frac{α}{2}-[β-(90°-\frac{α}{2})]=180°-(α+β)$,
∴D′B=D′C,∠BD′C=60°.
同(1)可证△AD′B≌△AD′C,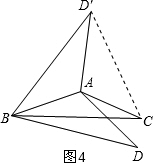
∴∠AD′B=∠AD′C,
∵∠AD′B+∠AD′C+∠BD′C=360°,
∴∠ADB=∠AD′B=150°,
(3)点D和点A在直线BC的异侧时,分三种情况讨论:
第一种情况:如图4,
当120°<α<180°时,连接CD′,
同理构建△ABD′≌△ABD,
∴∠DBA=∠D′BA,
同理可知:∠CBA=90°-$\frac{1}{2}$α,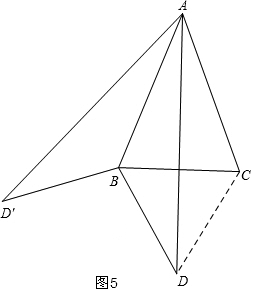
∴∠DBA=90°-$\frac{1}{2}$α+β,
∴∠DBA=∠D′BA=90°-$\frac{1}{2}$α+β,
∴∠CBD′=90°-$\frac{1}{2}$α+90°-$\frac{1}{2}$α+β=180°-α+β,
∵BD=BD′=BC,
∴当△D′BC为等边三角形时,∠AD′B=∠ADB=30°,
即180°-α+β=60°,
∴α-β=120°;
第二种情况:如图5,
当0°<α<120°时,连接CD,
∵BD=BD′=BC,
与图4同理可知:当△BDC是等边三角形时,
即β=60°,
此时△ABD≌△ACD,
则∠ADB=∠ADC=30°,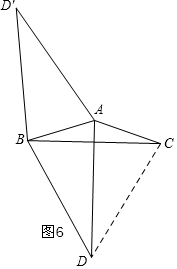
第三种情况:如图6,
当120°<α<180°时,连接CD,
同理构建△ABD′≌△ABD,
∵BD=BD′=BC,
当△BDC是等边三角形时,
即β=60°,
此时△ABD≌△ACD,
则∠ADB=∠ADC=30°,
综上所述,当满足0°<α<180°,β=60°或120°<α<180°,α-β=120°时,∠ADB=30°;
故答案为:0°<α<180°,β=60°或120°<α<180°时,α-β=120°.
点评 本题是几何变换的综合题,考查了等腰三角形、全等三角形、等边三角形边和角的关系;在等腰三角形中,已知一个角的度数,就能表示另外两个角的度数;同时本题还运用了分类讨论的思想,这在数学解题中是一个难点.


科目:初中数学 来源: 题型:选择题
| A. | 用抽样调查了解广州市中学生每周使用手机所用的时间 | |
| B. | 用全面调查了解某班学生对6月5日是“世界环境日”的知晓情况 | |
| C. | 用抽样调查选出某校短跑最快的学生参加全市比赛 | |
| D. | 用抽样调查了解南沙区初中学生零花钱的情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
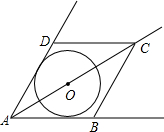 如图,菱形ABCD的边长为2,∠DAB=60°,点 O为射线AC上动点,动圆⊙O始终与射线AB相切,研究⊙O与菱形ABCD各边交点总个数的情况,以下论述正确的是( )
如图,菱形ABCD的边长为2,∠DAB=60°,点 O为射线AC上动点,动圆⊙O始终与射线AB相切,研究⊙O与菱形ABCD各边交点总个数的情况,以下论述正确的是( )| A. | ①②⑤ | B. | ② | C. | ①③④ | D. | ②④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
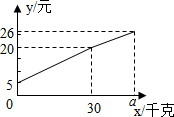 一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题:
一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,扇形OAB的圆心角∠AOB=120°,半径OA=6cm.
如图,扇形OAB的圆心角∠AOB=120°,半径OA=6cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com