
分析 (1)根据配方法的步骤先两边都除以2,移项,配方,开方即可得出两个一元一次方程,再求出方程的解即可;
(2)把a=1,b=-6,c=-4代入求根公式x=$\frac{{-b±\sqrt{{b^2}-4ac}}}{2a}$计算即可.
解答 解:(1)方程两边同除以2,得:x2+$\frac{5}{2}$x+$\frac{3}{2}$=0,
移项,得x2+$\frac{5}{2}x$=$-\frac{3}{2}$,
配方,得x2+$\frac{5}{2}$x+($\frac{5}{4}$)2=$-\frac{3}{2}$+($\frac{5}{4}$)2,
(x+$\frac{5}{4}$)2=$\frac{1}{16}$,
x+$\frac{5}{4}$=$\frac{1}{4}$或x+$\frac{5}{4}$=$-\frac{1}{4}$,
x1=-l;x2=$-\frac{3}{2}$;
(2)原方程可化为:x2-6x-4=0,
∵a=1,b=-6,c=-4;
∴x=$\frac{{-b±\sqrt{{b^2}-4ac}}}{2a}$=$\frac{{6±\sqrt{36-4×1×(-4)}}}{2×1}$=$\frac{{6±\sqrt{52}}}{2}$,
∴x=3±$\sqrt{13}$,
x1=3+$\sqrt{13}$,x2=3-$\sqrt{13}$;
点评 本题考查了配方法和公式法解一元二次方程,关键是能正确配方,配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.


科目:初中数学 来源: 题型:填空题
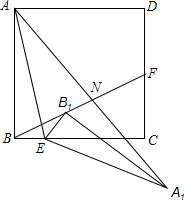 如图,正方形ABCD中,AB=4,点E是BC上靠近点B的四等分点,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在点A1位置处,连接AA1交BF于点N,则AN的长为$\frac{2\sqrt{85}}{5}$.
如图,正方形ABCD中,AB=4,点E是BC上靠近点B的四等分点,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在点A1位置处,连接AA1交BF于点N,则AN的长为$\frac{2\sqrt{85}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
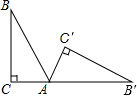 如图,在Rt△ABC中,∠B=30°,AC=1,将△ABC绕着点A按顺时针方向旋转到△AB′C′,使得B′落在CA的延长线上,则在旋转过程中,线段AB所扫过的面积为$\frac{4}{3}$π.
如图,在Rt△ABC中,∠B=30°,AC=1,将△ABC绕着点A按顺时针方向旋转到△AB′C′,使得B′落在CA的延长线上,则在旋转过程中,线段AB所扫过的面积为$\frac{4}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
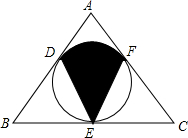 如图,已知等边△ABC的三边分别与⊙O相切于点D、E、F,若AB=2$\sqrt{3}$,则图中阴影部分的面积为$\frac{1}{3}$π+$\frac{\sqrt{3}}{2}$.(结果保留π)
如图,已知等边△ABC的三边分别与⊙O相切于点D、E、F,若AB=2$\sqrt{3}$,则图中阴影部分的面积为$\frac{1}{3}$π+$\frac{\sqrt{3}}{2}$.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com