
·ÖÎö £¨1£©Ôʽ·ÂÕÕÔĶÁ²ÄÁÏÖеķ½·¨Çó³öÖµ¼´¿É£»
£¨2£©Ôʽ·ÂÕÕÔĶÁ²ÄÁÏÖеķ½·¨Çó³öÖµ¼´¿É£»
£¨3£©ÔʽµÚÒ»¸öÀ¨ºÅÖзÂÕÕÔĶÁ²ÄÁÏÖеķ½·¨±äÐΣ¬¼ÆËã¼´¿ÉµÃµ½½á¹û£®
½â´ð ½â£º£¨1£©Ôʽ=$\frac{\sqrt{7}-\sqrt{6}}{£¨\sqrt{7}+\sqrt{6}£©£¨\sqrt{7}-\sqrt{6}£©}$=$\sqrt{7}$-$\sqrt{6}$£»
£¨2£©Ôʽ=$\frac{3\sqrt{2}-\sqrt{17}}{£¨3\sqrt{2}+\sqrt{17}£©£¨3\sqrt{2}-\sqrt{17}£©}$=3$\sqrt{2}$-$\sqrt{17}$£»
£¨3£©Ôʽ=£¨$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+¡+$\sqrt{2009}$-$\sqrt{2008}$+$\sqrt{2010}$-$\sqrt{2009}$£©•£¨1+$\sqrt{2010}$£©
=£¨$\sqrt{2010}$-1£©£¨$\sqrt{2010}$+1£©
=2010-1
=2009£®
µãÆÀ ´ËÌ⿼²éÁË·ÖĸÓÐÀí»¯£¬ÅªÇåÔĶÁ²ÄÁÏÖеķ½·¨ÊǽⱾÌâµÄ¹Ø¼ü£®


 ÌìÌìÏòÉÏÒ»±¾ºÃ¾íϵÁдð°¸
ÌìÌìÏòÉÏÒ»±¾ºÃ¾íϵÁдð°¸ СѧÉú10·ÖÖÓÓ¦ÓÃÌâϵÁдð°¸
СѧÉú10·ÖÖÓÓ¦ÓÃÌâϵÁдð°¸
| Ä꼶 | ¸ßÖÐ¿Î³Ì | Ä꼶 | ³õÖÐ¿Î³Ì |
| ¸ßÒ» | ¸ßÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ | ³õÒ» | ³õÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ß¶þ | ¸ß¶þÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õ¶þ | ³õ¶þÃâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ßÈý | ¸ßÈýÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õÈý | ³õÈýÃâ·Ñ¿Î³ÌÍƼö£¡ |
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | 10 | B£® | 11 | C£® | 12 | D£® | 13 |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÌî¿ÕÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÌî¿ÕÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÌî¿ÕÌâ
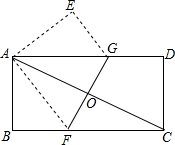 Èçͼ£¬½«Ò»¾ØÐÎֽƬABCDÕÛµþ£¬Ê¹Á½¸ö¶¥µãA£¬CÖغϣ¬ÕÛºÛΪFG..ÈôAB=8£¬BC=16£¬Ôò¡÷AEGµÄÃæ»ýΪ24£®
Èçͼ£¬½«Ò»¾ØÐÎֽƬABCDÕÛµþ£¬Ê¹Á½¸ö¶¥µãA£¬CÖغϣ¬ÕÛºÛΪFG..ÈôAB=8£¬BC=16£¬Ôò¡÷AEGµÄÃæ»ýΪ24£®²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
 Èçͼ£¬ADΪ¡÷ABCµÄÖÐÏߣ¬BEΪ¡÷ABDµÄÖÐÏߣ®
Èçͼ£¬ADΪ¡÷ABCµÄÖÐÏߣ¬BEΪ¡÷ABDµÄÖÐÏߣ®²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
°Ù¶ÈÖÂÐÅ - Á·Ï°²áÁбí - ÊÔÌâÁбí
ºþ±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨Æ½Ì¨ | ÍøÉÏÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | µçÐÅթƾٱ¨×¨Çø | ÉæÀúÊ·ÐéÎÞÖ÷ÒåÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com