
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 两点.
两点.
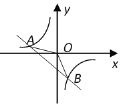
(1)试确定上述反比例函数和一次函数的表达式;
(2)求![]() 的面积.
的面积.
(3)根据图象写出反比例函数y≥n的x取值范围.
【答案】(1)反比例函数的解析式为![]() ;一次函数的解析式为y=-x-1;(2)
;一次函数的解析式为y=-x-1;(2)![]() ;(3)x<0或x≥1
;(3)x<0或x≥1
【解析】
(1)将点A的坐标代入反比例函数解析式中即可求出反比例函数的解析式,然后将点B的坐标代入反比例函数的解析式中即可求出n的值,最后将A、B的坐标代入一次函数解析式中即可求出一次函数的解析式;
(2)设直线AB与y轴交点为点C,过点A作AE⊥y轴于E,过点B作BF⊥y轴于F,求出点C的坐标,然后根据S△AOB=S△AOC+S△BOC即可求出结论;
(3)根据图象即可得出结论.
解:(1)将点A的坐标代入反比例函数![]() 中,得
中,得
![]()
解得:m=-2
∴反比例函数的解析式为![]()
将点B的坐标代入![]() 中,得
中,得
![]()
∴点B的坐标为(1,-2)
将![]() 代入一次函数
代入一次函数![]() 中,得
中,得
![]()
解得:![]()
∴一次函数的解析式为y=-x-1;
(2)设直线AB与y轴交点为点C,过点A作AE⊥y轴于E,过点B作BF⊥y轴于F
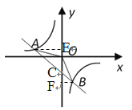
将x=0代入y=-x-1中,可得y=-1
∴点C的坐标为(0,-1)
∴OC=1
∵![]()
∴AE=2,BF=1
∴S△AOB=S△AOC+S△BOC
=![]()
=![]()
=![]()
(3)∵点B的纵坐标为n
∴反比例函数y≥n,应取点B的上方(含点B)
由图象可知:当x<0或x≥1时,反比例函数y≥n
∴反比例函数y≥n时,x<0或x≥1.


科目:初中数学 来源: 题型:
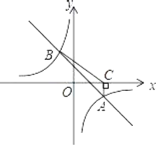
【题目】如图,已知一次函数y=﹣x+n的图象与反比例函数y=![]() 的图象交于A(4,﹣2),B(﹣2,m)两点.
的图象交于A(4,﹣2),B(﹣2,m)两点.
(1)请直接写出不等式﹣x+n≤![]() 的解集;
的解集;
(2)求反比例函数和一次函数的解析式;
(3)过点A作x轴的垂线,垂足为C,连接BC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.以下说法错误的是
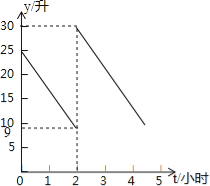
A.加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=﹣8t+25
B.途中加油21升
C.汽车加油后还可行驶4小时
D.汽车到达乙地时油箱中还余油6升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月20日,“美丽玉环,文旦飘香”号冠名列车正式发车,为广大旅客带去“中国文旦之乡”的独特味道.根据市场调查,在文旦上市销售的30天中,其销售价格![]() (元公斤)与第
(元公斤)与第![]() 天之间满足函数
天之间满足函数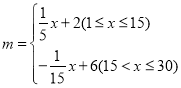 (其中
(其中![]() 为正整数);销售量
为正整数);销售量![]() (公斤)与第
(公斤)与第![]() 天之间的函数关系如图所示,如果文旦上市期间每天的其他费用为100元.
天之间的函数关系如图所示,如果文旦上市期间每天的其他费用为100元.
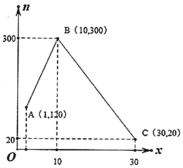
(1)求销售量![]() 与第
与第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)求在文旦上市销售的30天中,每天的销售利润![]() 与第
与第![]() 天之间的函数关系式;(日销售利润=日销售额-日维护费)
天之间的函数关系式;(日销售利润=日销售额-日维护费)
(3)求日销售利润![]() 的最大值及相应的
的最大值及相应的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
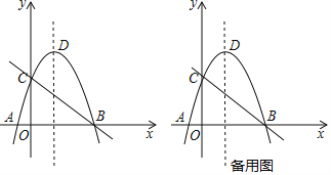
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴另一交点为
轴另一交点为![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,求
的值最小,求![]() 的最小值;
的最小值;
(3)在抛物线的对称轴上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知点A (﹣2,4)和点B (1,0)都在抛物线y=mx2+2mx+n上.
(1)求m、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AB′的交点为点C,试在x轴上找点D,使得以点B′、C、D为顶点的三角形与△ABC相似.

查看答案和解析>>
科目:初中数学 来源: 题型:
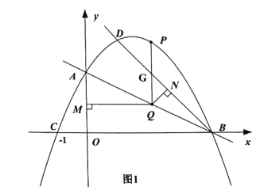
【题目】如图,一次函数![]() 的图像与坐标轴交于A、B两点,点C的坐标为
的图像与坐标轴交于A、B两点,点C的坐标为![]() ,二次函数
,二次函数![]() 的图像经过A、B、C三点.
的图像经过A、B、C三点.
(1)求二次函数的解析式
(2)如图1,已知点![]() 在抛物线上,作射线BD,点Q为线段AB上一点,过点Q作
在抛物线上,作射线BD,点Q为线段AB上一点,过点Q作![]() 轴于点M,作
轴于点M,作![]() 于点N,过Q作
于点N,过Q作![]() 轴交抛物线于点P,当QM与QN的积最大时,求点P的坐标;
轴交抛物线于点P,当QM与QN的积最大时,求点P的坐标;
(3)在(2)的条件下,连接AP,若点E为抛物线上一点,且满足![]() ,求点E的坐标.
,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
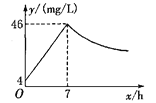
【题目】近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4 mg/L,此后浓度呈直线型增加,在第7小时达到最高值46 mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降,如图,根据题中相关信息回答下列问题:
(1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的CO浓度达到34 mg/L时,井下3 km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4 mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?
查看答案和解析>>
科目:初中数学 来源: 题型:
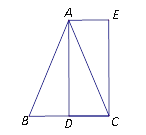
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() 于点
于点![]() ,把线段
,把线段![]() 沿着
沿着![]() 的方向平移
的方向平移![]() 得到线段
得到线段![]() ,连接
,连接![]() .
.
问:(1)四边形![]() 是_________形;
是_________形;
(2)若![]() 的周长比
的周长比![]() 的周长大6,求四边形
的周长大6,求四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com