
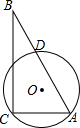
 如图,直角△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,已知:AC=6,BC=8,则⊙O的半径为$\frac{25}{8}$.
如图,直角△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,已知:AC=6,BC=8,则⊙O的半径为$\frac{25}{8}$. 分析 如图连接CD、OD、OC,延长DO交AC于E,设半径为R,先证明DE⊥AC,DE=$\frac{1}{2}$CB,在RT△OCE中,利用勾股定理即可解决问题.
解答 解:如图连接CD、OD、OC,延长DO交AC于E,设半径为R.
在RT△ABC中,∵∠ACB=90°,BC=8,AC=6,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵BD=AD=5,
∴CD=AD=5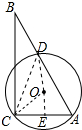 ,
,
∵DC=DA,
$\widehat{CD}$=$\widehat{AD}$,
∴DO⊥AC,EC=AE=3,
∴ED∥BC,∵BD=AD,
∴EC=EA,
∴DE=$\frac{1}{2}$BC=4,
在RT△COE中,∵∠OEC=90°,
∴CO2=OE2+CE2,
∴R2=(4-R)2+32,
∴R=$\frac{25}{8}$.
点评 本题考查点与圆的位置关系,三角形的中位线的性质,垂径定理、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | -$\frac{5}{2}$ | B. | -$\frac{2}{5}$ | C. | $\frac{5}{2}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
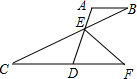 如图AB∥CD,AD与BC交于点E,EF平分∠BED交CD延长线于点F,若∠A=110°,∠B=30°,则∠F的度数是( )
如图AB∥CD,AD与BC交于点E,EF平分∠BED交CD延长线于点F,若∠A=110°,∠B=30°,则∠F的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
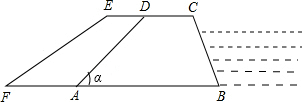 如图,某堤坝的横截面是梯形ABCD,背水坡AD的坡度(即tanα)为1:1.2,坝高10米,为了提高坝的防洪能力,由相关部门决定加固堤坝,要求将坝顶CD加宽2米,形成新的背水坡EF,其坡度为1:1.4,已知堤坝总长度为1000米.
如图,某堤坝的横截面是梯形ABCD,背水坡AD的坡度(即tanα)为1:1.2,坝高10米,为了提高坝的防洪能力,由相关部门决定加固堤坝,要求将坝顶CD加宽2米,形成新的背水坡EF,其坡度为1:1.4,已知堤坝总长度为1000米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
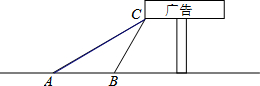 如图,某学校数学兴趣小组想了解“第25届世界技巧锦标赛倒计时”广告牌的高度,他们在A点处测得广告牌底端C点的仰角为30°,然后向广告牌前进10m到达点B处,又测得C点的仰角为60°.请你根据以上数据求广告牌底端C点离地面的高度.(结果保留根号)
如图,某学校数学兴趣小组想了解“第25届世界技巧锦标赛倒计时”广告牌的高度,他们在A点处测得广告牌底端C点的仰角为30°,然后向广告牌前进10m到达点B处,又测得C点的仰角为60°.请你根据以上数据求广告牌底端C点离地面的高度.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起,据试验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起,据试验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com