
在平面直角坐标系中,二次函数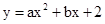 的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的关系解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
考生注意:下面的(3)、(4)、(5)题为三选一的选做题,即只能选做其中一个题目,多答时只按作答的首题评分,切记啊!
(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由;
(4)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
(5)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
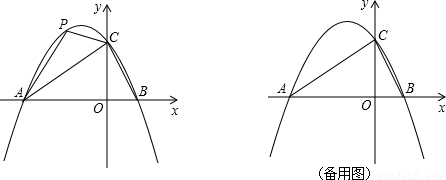
(1) (2)存在点
(2)存在点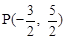 ,使△ACP的面积最大(3)存在。点
,使△ACP的面积最大(3)存在。点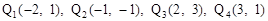 (4)存在。点
(4)存在。点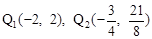 。(5)点
。(5)点
【解析】解:(1)由抛物线 过A(-3,0),B(1,0),则
过A(-3,0),B(1,0),则
 ,解得
,解得 。
。
∴二次函数的关系解析式为 。
。
(2)设点P坐标为(m,n),则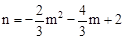 。
。
连接PO,作PM⊥x轴于M,PN⊥y轴于N。
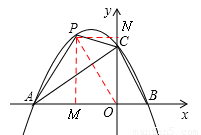
PM =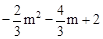 ,
, 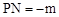 ,AO=3。
,AO=3。
当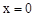 时,
时,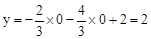 ,所以OC=2。
,所以OC=2。
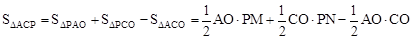 111
111
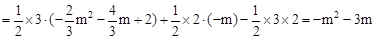
∵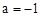 <0,∴函数
<0,∴函数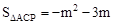 有最大值,当
有最大值,当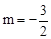 时,
时,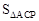 有最大值。
有最大值。
此时 。
。
∴存在点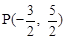 ,使△ACP的面积最大。
,使△ACP的面积最大。
(3)存在。点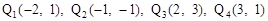 。
。
(4)存在。点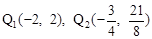 。
。
(5)点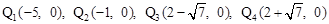 。
。
(1)将点A、B的坐标代入 即可求得a、b,从而得到二次函数的关系解析式。
即可求得a、b,从而得到二次函数的关系解析式。
(2)设点P坐标为(m,n),则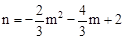 。连接PO,作PM⊥x轴于M,PN⊥y轴于N,根据
。连接PO,作PM⊥x轴于M,PN⊥y轴于N,根据 求出S关于m的二次函数,根据二次函数最值求法即可求解。
求出S关于m的二次函数,根据二次函数最值求法即可求解。
(3)分BQ为斜边和CQ为斜边两种情况讨论即可。
(4)分△BQE∽△AOC,△EBQ∽△AOC,△QEB∽△AOC三种情况讨论即可。
(5)分AC是边和对角线两种情况讨论即可。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com