

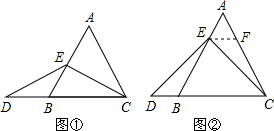
分析 (1)①如图1,由题可得BD=CE=t,易证△BDC≌△CEA,则有∠BCD=∠CAE,根据三角形外角的性质可求得∠EFC=60°,即可得到∠AFC=120°;②延长FD到G,使得FG=FA,连接GA、GB,过点B作BH⊥FG于H,如图2,易证△FAG是等边三角形,结合△ABC是等边三角形可证到△AGB≌△AFC,则有GB=FC,∠AGB=∠AFC=120°,从而可得∠BGF=60°.设AF=x,FC=y,则有FG=AF=x,BG=CF=y.在Rt△BHG中运用三角函数可得BH=$\frac{\sqrt{3}}{2}$y,GH=$\frac{1}{2}$y,从而有FH=x-$\frac{1}{2}$y.在Rt△BHF中根据勾股定理可得BF2=x2-xy+y2,代入所求代数式就可解决问题;
(2)过点E作EN⊥AB于N,连接MC,如图3,由题可得∠BEN=30°,BD=t,CE=2t-6,从而有BE=12-2t,BN=6-t,进而可得DN=EC.由△DEM是等边三角形可得DE=EM,∠DEM=60°,从而可得∠NDE=∠MEC,进而可证到△DNE≌△ECM,则有∠DNE=∠ECM=90°,故M点运动的路径为过点C垂直于BC的一条线段.
然后只需确定点M的始点和终点位置,就可解决问题.
解答 解:(1)如图1,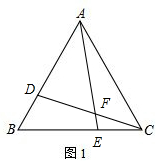
由题可得BD=CE=t.
∵△ABC是等边三角形,
∴BC=AC,∠B=∠ECA=60°.
在△BDC和△CEA中,
$\left\{\begin{array}{l}{BD=CE}\\{∠B=∠ECA}\\{BC=AC}\end{array}\right.$,
∴△BDC≌△CEA,
∴∠BCD=∠CAE,
∴∠EFC=∠CAE+∠ACF=∠BCD+∠ACF=∠ACB=60°,
∴∠AFC=120°;
②延长FD到G,使得FG=FA,连接GA、GB,过点B作BH⊥FG于H,如图2,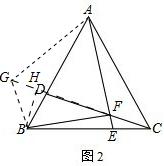
∵∠AFG=180°-120°=60°,FG=FA,
∴△FAG是等边三角形,
∴AG=AF=FG,∠AGF=∠GAF=60°.
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠GAF=∠BAC,
∴∠GAB=∠FAC.
在△AGB和△AFC中,
$\left\{\begin{array}{l}{AG=AF}\\{∠GAB=∠FAC}\\{AB=AC}\end{array}\right.$,
∴△AGB≌△AFC,
∴GB=FC,∠AGB=∠AFC=120°,
∴∠BGF=60°.
设AF=x,FC=y,
则有FG=AF=x,BG=CF=y.
在Rt△BHG中,
BH=BG•sin∠BGH=BG•sin60°=$\frac{\sqrt{3}}{2}$y,
GH=BG•cos∠BGH=BG•cos60°=$\frac{1}{2}$y,
∴FH=FG-GH=x-$\frac{1}{2}$y.
在Rt△BHF中,BF2=BH2+FH2
=($\frac{\sqrt{3}}{2}$y)2+(x-$\frac{1}{2}$y)2=x2-xy+y2.
∴$\frac{{A{F^2}+F{C^2}-B{F^2}}}{AF•FC}$=$\frac{{x}^{2}+{y}^{2}-({x}^{2}-xy+{y}^{2})}{xy}$=1;
(2)过点E作EN⊥AB于N,连接MC,如图3,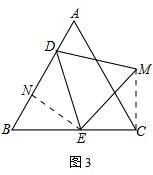
由题可得:∠BEN=30°,BD=1×t=t,CE=2(t-3)=2t-6.
∴BE=6-(2t-6)=12-2t,BN=BE•cosB=$\frac{1}{2}$BE=6-t,
∴DN=t-(6-t)=2t-6,
∴DN=EC.
∵△DEM是等边三角形,
∴DE=EM,∠DEM=60°.
∵∠NDE+∠NED=90°,∠NED+∠MEC=180°-30°-60°=90°,
∴∠NDE=∠MEC.
在△DNE和△ECM中,
$\left\{\begin{array}{l}{DN=EC}\\{∠NDE=∠CEM}\\{DE=EM}\end{array}\right.$,
∴△DNE≌△ECM,
∴∠DNE=∠ECM=90°,
∴M点运动的路径为过点C垂直于BC的一条线段.
当t=3时,E在点B,D在AB的中点,
此时CM=EN=CD=BC•sinB=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$;
当t=6时,E在点C,D在点A,
此时点M在点C.
∴当3≤t≤6时,M点所经历的路径长为3$\sqrt{3}$.
点评 本题主要考查了等边三角形的判定与性质、全等三角形的判定与性质、锐角三角函数、特殊角的三角函数值、勾股定理、三角形外角的性质等知识,综合性比较强,有一定的难度;构造旋转型全等三角形(由共顶点的两个等边三角形组成)是解决第1(2)小题的关键,证到∠ECM=90°是解决第(2)小题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
 已知y=$\frac{1}{2}$x2+2x+1
已知y=$\frac{1}{2}$x2+2x+1 查看答案和解析>>
科目:初中数学 来源: 题型:选择题
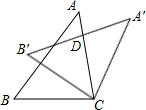 如图,把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A度数为( )
如图,把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A度数为( )| A. | 48° | B. | 58° | C. | 68° | D. | 78° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com