
 (180°-∠APB)=
(180°-∠APB)= ∠MON=∠BOP,可证△PBC∽△POB,由S△POB=3S△PCB可知,PO=3PC,再利用相似比求解;
∠MON=∠BOP,可证△PBC∽△POB,由S△POB=3S△PCB可知,PO=3PC,再利用相似比求解;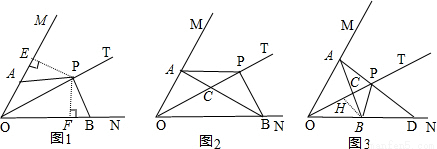 解:(1)作PE⊥OM,PF⊥ON,垂足为E、F
解:(1)作PE⊥OM,PF⊥ON,垂足为E、F (180°-∠APB)=
(180°-∠APB)= ∠MON=∠BOP,
∠MON=∠BOP,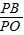 =
=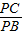 ,
,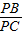 =
=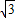
 (180°-∠APB)=30°,
(180°-∠APB)=30°, (180°-30°)=75°,则∠OBP=∠ABO+∠ABP=105°,
(180°-30°)=75°,则∠OBP=∠ABO+∠ABP=105°, OB=1,OH=
OB=1,OH=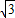 ,
,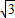 +1.
+1.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
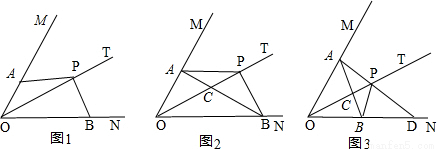
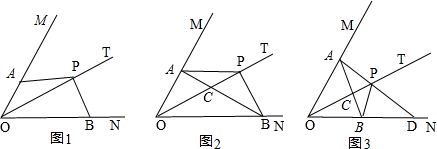
已知, 点P是∠MON的平分线上的一动点,射线PA交射线OM于点A,将射线PA绕点P逆时针旋转交射线ON于点B,且使∠APB+∠MON=180°.
(1)利用图1,求证:PA=PB;
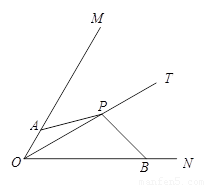
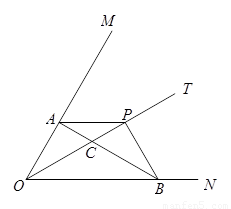
(2)如图2,若点![]() 是
是![]() 与
与![]() 的交点,当
的交点,当![]() 时,求PB与PC的比值;
时,求PB与PC的比值;
(3)若∠MON=60°,OB=2,射线AP交ON于点![]() ,且满足且
,且满足且![]() ,请借助图3补全图形,并求
,请借助图3补全图形,并求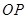 的长.
的长.
(1)(2)
(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
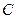 是
是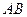 与
与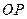 的交点,当
的交点,当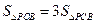 时,求PB与PC的比值;
时,求PB与PC的比值;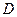 ,且满足且
,且满足且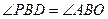 ,请借助图3补全图形,并求
,请借助图3补全图形,并求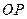 的长.
的长.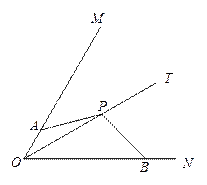 (2)
(2)

查看答案和解析>>
科目:初中数学 来源:2010-2011学年北京市考数学一模试卷 题型:解答题
已知, 点P是∠MON的平分线上的一动点,射线PA交射线OM于点A,将射线PA绕点P逆时针旋转交射线ON于点B,且使∠APB+∠MON=180°.
(1)利用图1,求证:PA=PB;
(2)如图2,若点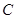 是
是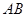 与
与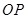 的交点,当
的交点,当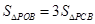 时,求PB与PC的比值;
时,求PB与PC的比值;
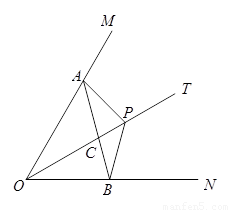
(3)若∠MON=60°,OB=2,射线AP交ON于点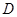 ,且满足且
,且满足且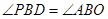 ,请借助图3补全图形,并求
,请借助图3补全图形,并求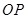 的长.
的长.
(1) (2)
(2)
(3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com