
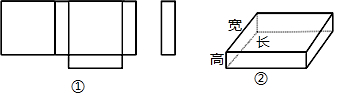
���� ��1������ƽ��ͼ�εó��������������
��2�����ݳ������չ��ͼ�������֪�����������
��3�����ݳ�����������ʽ���ɵô𰸣�
��� �⣨1��С��������8���⣬
�ʴ�Ϊ��8��
��2����ͼ�����������
��3��6��6��2=72cm3��
���������ֽ�е������72cm3��
���� ������Ҫ�����˼���չ��ͼ����Ͼ�������⣬�����������չ��ͼ��ͨ���������ͼ����ƽ��ͼ�ε�ת���������ռ����ǽ����������Ĺؼ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a6b2 | B�� | a2b5 | C�� | a5b3 | D�� | a3b6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
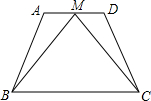 ��ͼ������ABCD�У�AD��BC����M��AD���е㣬��MB=MC����AD=4��AB=6��BC=8��������ABCD���ܳ�Ϊ24��
��ͼ������ABCD�У�AD��BC����M��AD���е㣬��MB=MC����AD=4��AB=6��BC=8��������ABCD���ܳ�Ϊ24���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
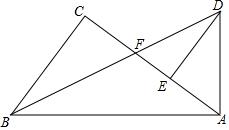 ��ͼ����Rt��ABC��Rt��ABD�У���C=��BAD=90�㣬BD��AC���ڵ�F����AF=AD����DE��AC�ڵ�E��
��ͼ����Rt��ABC��Rt��ABD�У���C=��BAD=90�㣬BD��AC���ڵ�F����AF=AD����DE��AC�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
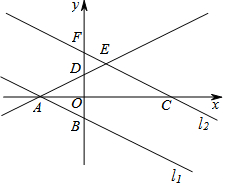 ��ֱ֪��l1��y=-$\frac{1}{2}$x-1�ֱ���x��y�ύ�ڵ�A��B����ֱ��l1ƽ�ƺ����C��4��0���õ�ֱ��l2��l2��ֱ��AD�ڵ�E����y���ڵ�F����EA=EC��
��ֱ֪��l1��y=-$\frac{1}{2}$x-1�ֱ���x��y�ύ�ڵ�A��B����ֱ��l1ƽ�ƺ����C��4��0���õ�ֱ��l2��l2��ֱ��AD�ڵ�E����y���ڵ�F����EA=EC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
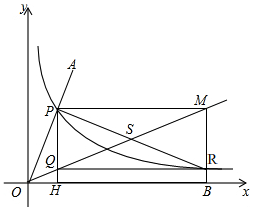 ��ͼ����ƽ��ֱ������ϵ�У�����OA������������y=$\frac{1}{x}$��x��0��ͼ���ڵ�P����RΪ����������y=$\frac{1}{x}$��x��0��ͼ���ϵ���һ�㣬��PR=2OP���ֱ����P��R��x�ᡢy���ƽ���ߣ������ཻ�ڵ�M��a��b����ֱ��MR��x���ڵ�B������P��y���ƽ���߷ֱ�ֱ��OM��x���ڵ�Q��H������RQ��
��ͼ����ƽ��ֱ������ϵ�У�����OA������������y=$\frac{1}{x}$��x��0��ͼ���ڵ�P����RΪ����������y=$\frac{1}{x}$��x��0��ͼ���ϵ���һ�㣬��PR=2OP���ֱ����P��R��x�ᡢy���ƽ���ߣ������ཻ�ڵ�M��a��b����ֱ��MR��x���ڵ�B������P��y���ƽ���߷ֱ�ֱ��OM��x���ڵ�Q��H������RQ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com