练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．

    证明见解析.

    解析试题分析：根据平行线的性质可知∠AED=∠C，∠A=∠FEC，根据相似三角形的判定定理可知△ADE∽△EFC．
    试题解析：∵DE∥BC，∴DE∥FC. ∴∠AED=∠C．
    又∵EF∥AB，∴EF∥AD. ∴∠A=∠FEC．
    ∴△ADE∽△EFC．
    考点：1.平行线的性质；2.相似三角形的判定．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    网格中每个小正方形的边长都是1.
    (1)将图1中画一个格点三角形DEF，使得△DEF≌△ABC

    (2)将图2中画一个格点三角形MNL，使得△MNL∽△ABC,且相似比为2:1

    (3)将图3中画一个格点三角形OPQ，使得△OPQ∽△ABC，且相似比为:1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图,△ABC中，∠C=90°，BC=8cm，，点P从B点出发，沿BC方向以2cm/m的速度移动，点Q从C出发，沿CA方向以1cm/m的速度移动。若P、Q同时分别从B、C出发，经过多少时间△CPQ与△CBA相似？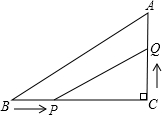

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在正方形ABCD中，E、F分别是边AD、CD上的点，AE=ED，DF=DC，连结并延长交的延长线于点

    （1）求证：△ABE∽△DEF；
    （2）若正方形的边长为4，求BG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图1，矩形ABCD中，AB=21，AD=12，E是CD边上的一点，CE=5，M是BC边上的中点，动点P从点A出发，沿AB边以每秒1个单位长度的速度向终点B运动，连结PM.设动点P的运动时间是t秒.

    （1）求线段AE的长；
    （2）当△ADE与△PBM相似时，求t的值；
    （3）如图2，连接EP，过点P作PH⊥AE于H．①当EP平分四边形PMEH的面积时，求t的值；②以PE为对称轴作线段BC的轴对称图形B′C′，当线段B′C′与线段AE有公共点时，写出t的取值范围（直接写出答案）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在△ABC中，D、E两点分别在AC、AB两边上，∠ABC=∠ADE，AB=7，AD=3，AE=2.7,求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    【提出问题】
    （1）如图1，在等边△ABC中，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等边△AMN，连结CN．求证：∠ABC=∠ACN．

    【类比探究】
    （2）如图2，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，（1）中结论∠ABC=∠ACN还成立吗？请说明理由．

    【拓展延伸】
    （3）如图3，在等腰△ABC中，BA=BC，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等腰△AMN，使顶角∠AMN=∠ABC．连结CN．试探究∠ABC与∠ACN的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    在矩形ABCD中，点P是边AD上的动点，连接BP，线段BP的垂直平分线交边BC于点Q，垂足为点M，连接QP（如图）．已知AD=13，AB=5，设AP=x，BQ=y．

    （1）求y关于x的函数解析式，并写出x的取值范围；
    （2）当以AP长为半径的⊙P和以QC长为半径的⊙Q外切时，求x的值；
    （3）点E在边CD上，过点E作直线QP的垂线，垂足为F，如果EF=EC=4，求x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    如图，几何体的主视图是（　　）

    A． B． C． D． 

    查看答案和解析>>

    同步练习册答案