
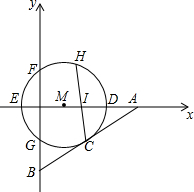
 如图,直线y=$\frac{\sqrt{3}}{3}$x-$\frac{5\sqrt{3}}{3}$与x轴、y轴分别交于点A,B两点.点M为x轴上一点,以M为圆心,2为半径作圆,⊙M恰好与直线y=$\frac{\sqrt{3}}{3}$x-$\frac{5\sqrt{3}}{3}$相切,切点为C.设⊙M与x轴、y轴分别交于D、E、G、F,H为⊙M上一点,连结HC交x轴于点I.给出下列结论:①OA=5;②∠BAO=30°;③点M的坐标为(1,0);④CD=2;⑤若EI:IC=3:2,则cos∠HCD=$\frac{3}{5}$.其中正确的有①②③④.
如图,直线y=$\frac{\sqrt{3}}{3}$x-$\frac{5\sqrt{3}}{3}$与x轴、y轴分别交于点A,B两点.点M为x轴上一点,以M为圆心,2为半径作圆,⊙M恰好与直线y=$\frac{\sqrt{3}}{3}$x-$\frac{5\sqrt{3}}{3}$相切,切点为C.设⊙M与x轴、y轴分别交于D、E、G、F,H为⊙M上一点,连结HC交x轴于点I.给出下列结论:①OA=5;②∠BAO=30°;③点M的坐标为(1,0);④CD=2;⑤若EI:IC=3:2,则cos∠HCD=$\frac{3}{5}$.其中正确的有①②③④. 分析 ①正确.求出点A坐标即可判断.
②正确.求出tan∠BAO的值即可判断.
③正确.在Rt△AMC中,根据30度角性质求出AM,即可解决问题.
④正确.只要证明△MCD是等边三角形即可.
⑤错误.由△EIH∽△CID,得到$\frac{EH}{CD}$=$\frac{EI}{IC}$=$\frac{3}{2}$,求出EH,再根据cos∠HCD=cos∠HED=$\frac{EH}{ED}$=$\frac{3}{4}$即可判断.
解答 解:如图,连接CD、HD、EH.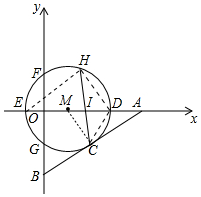
∵直线y=$\frac{\sqrt{3}}{3}$x-$\frac{5\sqrt{3}}{3}$与x轴、y轴分别交于点A,B两点,
令x=0,则y=-$\frac{5\sqrt{3}}{3}$,令y=0则x=5,
∴A(5,0),B(0,-$\frac{5\sqrt{3}}{3}$),
∴OA=5,OB=$\frac{5\sqrt{3}}{3}$故①正确,
∵tan∠BAO=$\frac{OB}{OA}$=$\frac{\sqrt{3}}{3}$,
∴∠BAO=30°.故②正确
∵⊙M与AB相切于点C,
∴CM⊥AC,
∴∠ACM=90°,∵∠CAM=30°,
∴AM=2CM=4,
∴OM=OA-AM=1,
∴点M坐标(1,0)故③正确,
∵∠AMC=90°-∠CAM=60°,MC=DM,
∴△MCD是等边三角形,
∴CD=CM=2,故④正确,
∵∠HEI=∠DCI,∠EIH=∠CID,
∴△EIH∽△CID,
∴$\frac{EH}{CD}$=$\frac{EI}{IC}$=$\frac{3}{2}$,
∴$\frac{EH}{2}$=$\frac{3}{2}$,
∴EH=3,
∵ED是直径,
∴∠EHD=90°,
∴cos∠HCD=cos∠HED=$\frac{EH}{ED}$=$\frac{3}{4}$,
故⑤错误.
故答案为①②③④.
点评 本题考查圆综合题、一次函数、相似三角形的判定和性质、锐角三角函数、直角三角形30度角性质、等边三角形的判定和性质等知识,解题的关键是灵活运用这些知识解决问题,学会用转化的思想思考问题,属于中考压轴题.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0).在点F运动过程中,设OE=a,OF=b,用含a的代数式表示b为b=a+2.
已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0).在点F运动过程中,设OE=a,OF=b,用含a的代数式表示b为b=a+2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com