

分析 (1)Rt△AOB≌Rt△CED且直角边为6,所以有A(0,6),B(6,0),D(-6,0),
(2)Rt△CED沿x轴以每秒2个单位长的速度向右运动,且DE=6,所以在运动过程中有两种情况,即D点仍停留在y轴左侧和D在y轴右侧,需分情况讨论.在第一种情况中,重合部分为两个全等的直角梯形,在第二种情况中,重合部分为一个等腰直角三角形,面积易求出.
(3)当运动时间为4秒时,即为(2)中第二种情况,此时G(4,2).
解答 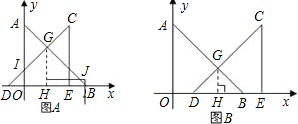 解:(1)因为两个直角边为6的全等的等腰Rt△AOB和Rt△CED中,
解:(1)因为两个直角边为6的全等的等腰Rt△AOB和Rt△CED中,
可得:A(0,6),B(6,0),D(-6,0).
(2)当0≤x<3时,位置如图A所示,
作GH⊥DB,垂足为H,可知:OE=2x,EH=x,
DO=6-2x,DH=6-x,
∴y=2S梯形IOHG=2(S△GHD-S△IOD)
=2[$\frac{1}{2}$(6-x)2-$\frac{1}{2}$(6-2x)2]
=2($\frac{3}{2}$x2+6x)
=-3x2+12x
当3≤x≤6时,位置如图B所示.
可知:DB=12-2x
∴y=S△DGB=$\frac{1}{2}$($\frac{\sqrt{2}}{2}$DB)2=$\frac{1}{2}$[$\frac{\sqrt{2}}{2}$(12-2x)]2=x2-12x+36
∴y与x的函数关系式为:y=$\left\{\begin{array}{l}{-3{x}^{2}+12x(0≤x<3)}\\{{x}^{2}-12x+36(3≤x≤6)}\end{array}\right.$;
(3)图B中,作GH⊥OE,垂足为H,
当x=4时,OE=2x=8,DB=12-2x=4,
∴GH=DH=$\frac{1}{2}$DB=2,OH=6-HB=6-$\frac{1}{2}$DB=6-2=4
∴G(4,2).
点评 此题考查三角形综合题,关键是把运动问题和二次函数紧密联系,考虑问题要全面.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
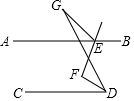 如图,已知AB∥CD,点E为AB上一点,∠CDF=∠FDG,FE平分∠BEG,则∠F与∠G之间满足的数量关系是( )
如图,已知AB∥CD,点E为AB上一点,∠CDF=∠FDG,FE平分∠BEG,则∠F与∠G之间满足的数量关系是( )| A. | ∠F+∠G=90° | B. | 2∠G+∠F=180° | C. | ∠F-∠G=90° | D. | 2∠F-∠G=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m-7<n-7 | B. | 3m<3n | C. | -5m>-5n | D. | $\frac{m}{9}$>$\frac{n}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对常州市居民日平均用水量的调查 | |
| B. | 对一批LED节能灯使用寿命的调查 | |
| C. | 对常州新闻频道“政风热线”栏目收视率的调查 | |
| D. | 对某校八年级(2)班同学的视力情况的调查 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com