
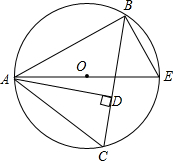
 如图,△ABC内接于⊙O,AD是△ABC的边BC上的高,AE是⊙O的直径,连接BE,求证:AB•AC=AD•AE.
如图,△ABC内接于⊙O,AD是△ABC的边BC上的高,AE是⊙O的直径,连接BE,求证:AB•AC=AD•AE.  新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:填空题
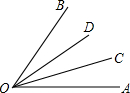 如图所示,如果OC,OD是∠AOB的三等分线,那么∠AOC=∠BOD=∠DOC,∠BOD=$\frac{1}{3}$∠AOB,∠AOD=22∠BOD或2∠DOC或2∠COA.
如图所示,如果OC,OD是∠AOB的三等分线,那么∠AOC=∠BOD=∠DOC,∠BOD=$\frac{1}{3}$∠AOB,∠AOD=22∠BOD或2∠DOC或2∠COA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
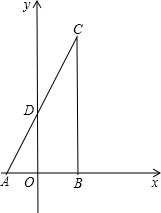 已知△ABC中,∠B=90°,∠A=60°,AB=6,把它放在平面坐标系中,使A,B两点关于y轴对称,边AC交y轴于点D,如图所示,点P是AC边上的动点,点E是x轴上的动点,且PB=PE,设PA=t,
已知△ABC中,∠B=90°,∠A=60°,AB=6,把它放在平面坐标系中,使A,B两点关于y轴对称,边AC交y轴于点D,如图所示,点P是AC边上的动点,点E是x轴上的动点,且PB=PE,设PA=t,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
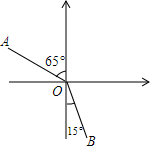 如图所示,按要求回答下列问题:
如图所示,按要求回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知C、D是线段AB上的两点,且AC=$\frac{1}{3}$AB,BD=$\frac{1}{3}$BC,图中一共有6条线段,若AC=3,则CD的长度为4.
如图,已知C、D是线段AB上的两点,且AC=$\frac{1}{3}$AB,BD=$\frac{1}{3}$BC,图中一共有6条线段,若AC=3,则CD的长度为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间(小时) | 5 | 10 | 15 | 20 | 25 |
| 计时制的费用(元) | 21 | 42 | 63 | 84 | 105 |
| 包月制的费用(元) | 54 | 60 | 66 | 72 | 78 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com