
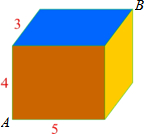
 如图所示,有一个长方体,它的长、宽、高分别为5cm,3cm,4cm.在顶点A处有一只蚂蚁,它想吃到与顶点A相对的顶点B的食物.
如图所示,有一个长方体,它的长、宽、高分别为5cm,3cm,4cm.在顶点A处有一只蚂蚁,它想吃到与顶点A相对的顶点B的食物.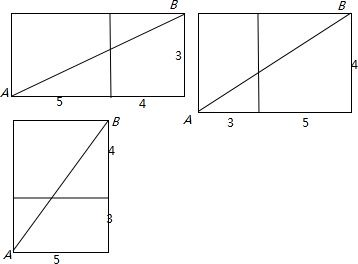 从长方体的一条对角线的一个端点A出发,沿表面运动到另一个端点B,有三种方案,如图是它们的三种部分侧面展开图,
从长方体的一条对角线的一个端点A出发,沿表面运动到另一个端点B,有三种方案,如图是它们的三种部分侧面展开图,| 80 |
| 74 |
| 90 |
| 74 |
| 74 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是49,小正方形的面积4,直角三角形的两直角边长分别为a,b,那么下列结论正确的有( )个.
我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是49,小正方形的面积4,直角三角形的两直角边长分别为a,b,那么下列结论正确的有( )个.| 94 |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是49,小正方形的面积4,直角三角形的两直角边长分别为a,b,那么下列结论正确的有____个.
我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是49,小正方形的面积4,直角三角形的两直角边长分别为a,b,那么下列结论正确的有____个.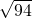 .
.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是小方家厨房设计装修的俯视图,尺寸如图所示,DF边上有一个80cm宽的门,留下墙DE长为200cm.冰箱摆放在图纸中的位置,冰箱的俯视图是一个边长为60cm的正方形,为了利于冰箱的散热,冰箱的后面和侧面离开墙面都至少留有10cm的空隙.
如图,是小方家厨房设计装修的俯视图,尺寸如图所示,DF边上有一个80cm宽的门,留下墙DE长为200cm.冰箱摆放在图纸中的位置,冰箱的俯视图是一个边长为60cm的正方形,为了利于冰箱的散热,冰箱的后面和侧面离开墙面都至少留有10cm的空隙.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com