

分析 (1)根据三角形内角和定理计算即可;
(2)根据翻转变换的性质和三角形内角和定理计算;
(3)根据翻转变换的性质和三角形的外角的性质解答.
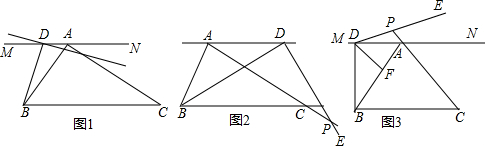
解答 解:(1)∠1+∠2=∠B+∠C.
∵∠A+∠1+∠2=180°,∠A+∠B+∠C=180°,
∴∠1+∠2=∠B+∠C,
当∠A=40°时,∠B+∠C=180°-40°=140°,∠1+∠2=180°-40°=140°,
∴∠B+∠C+∠1+∠2=280°,
故答案为:280°;
(2)由(1)得,∠ADE+∠AED=∠B+∠C,
由翻折变换的性质可知,∠1+∠2=∠ADE+∠AED,
∴∠1+∠2=∠B+∠C,
由翻折变换的性质可知,∠ADE=∠A′DE,∠AED=∠A′ED,
∠ADE+∠AED=180°-∠A,
∠ADA′+∠AEA′=360°-2∠A,
∠A′DB+∠A′EC=360°-(360°-2∠A)=2∠A
当∠A=30°时,∠A′DB+∠A′EC=60°,
故答案为:60°;∠A′DB+∠A′EC=2∠A;
(3)∠A'DB=∠A+∠AFD,∠AFD=∠A′+∠A'EC,
∴∠A′DB=∠A′EC+2∠A,
故答案为:∠A′DB=∠A′EC+2∠A.
点评 本题考查的是翻转变换的性质,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com