
【题目】要在一块长52m,宽48m的矩形绿地上,修建同样宽的两条互相垂直的甬路.下面分别是小亮和小颖的设计方案. 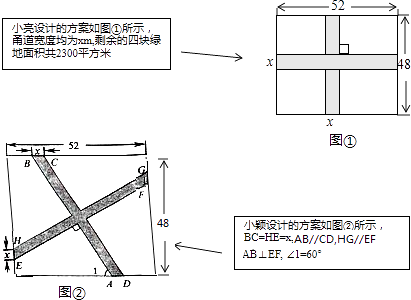
(1)求小亮设计方案中甬路的宽度x;
(2)求小颖设计方案中四块绿地的总面积(友情提示:小颖设计方案中的x与小亮设计方案中的x取值相同)
【答案】
(1)解:根据小亮的设计方案列方程得:(52﹣x)(48﹣x)=2300
解得:x=2或x=98(舍去)
∴小亮设计方案中甬道的宽度为2m
(2)解:作AI⊥CD,垂足为I,
∵AB∥CD,∠1=60°,
∴∠ADI=60°,
∵BC∥AD,
∴四边形ADCB为平行四边形,
∴BC=AD
由(1)得x=2,
∴BC=HE=2=AD
在Rt△ADI中,AI=2sin60°= ![]()
∴小颖设计方案中四块绿地的总面积为52×48﹣52×2﹣48×2+( ![]() )2=2299平方米.
)2=2299平方米.

【解析】(1)根据小亮的方案表示出矩形的长和宽,利用矩形的面积公式列出方程求解即可;(2)求得甬道的宽后利用平行四边形的面积计算方法求得两个阴影部分面积的和即可;


科目:初中数学 来源: 题型:
【题目】射击队为从甲、乙两名运动员选拔一人参加运动会,对他们进行了六次测试,测试成绩如下表(单位:环)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)由表格中的数据,计算出甲的平均成绩是 环,乙的成绩是 环.
(2)结合平均水平与发挥稳定性你认为推荐谁参加比赛更适合,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的情景对话,然后解答问题:
老师:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小明:那直角三角形是否存在奇异三角形呢?
小红:等边三角形一定是奇异三角形.
(1)根据“奇异三角形”的定义,小红得出命题:“等边三角形一定是奇异三角形”,则小红提出的命题是 .(填“真命题”或“假命题”)
(2)若![]() 是奇异三角形,其中两边的长分别为
是奇异三角形,其中两边的长分别为![]() 、
、![]() ,则第三边的长为 .
,则第三边的长为 .
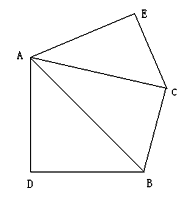
(3)如图,![]() 中,
中,![]() ,以
,以![]() 为斜边作等腰直角三角形
为斜边作等腰直角三角形![]() ,点
,点![]() 是
是![]() 上方的一点,且满足
上方的一点,且满足![]() .求证:
.求证:![]() 是奇异三角形.
是奇异三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=x+4分别与x轴、y轴相交于点M,N,边长为2的正方形OABC一个顶点O在坐标系的原点,直线AN与MC相交于点P,若正方形绕着点O旋转一周,则点P到点(0,2)长度的最小值是( ) 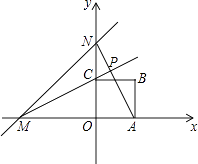
A.2 ![]() ﹣2
﹣2
B.3﹣2 ![]()
C.![]()
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】a![]() b是新规定的一种运算法则:a
b是新规定的一种运算法则:a![]() b=a2+ab,例如3
b=a2+ab,例如3![]() (﹣2)=32+3×(﹣2)=3.
(﹣2)=32+3×(﹣2)=3.
(1)求(﹣3)![]() 5的值;
5的值;
(2)若(﹣2)![]() x=6,求x的值;
x=6,求x的值;
(3)若3![]() (2
(2![]() x)=﹣4+x,求x的值.
x)=﹣4+x,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com