
【题目】如图,一个粒子在第一象限内及x轴,y轴上运动,第1分钟从原点运动到![]() ,第2分钟从
,第2分钟从![]() 运动到
运动到![]() ,而后它接着按图中箭头所示的与x轴y轴平行的方向来回运动,且每分钟移动1个长度单位.在第2019分钟时,这个粒子所在位置的坐标是( )
,而后它接着按图中箭头所示的与x轴y轴平行的方向来回运动,且每分钟移动1个长度单位.在第2019分钟时,这个粒子所在位置的坐标是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥AB交AB于N,交AC于N,若BM+CN=8,则线段MN的长为( )
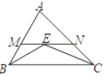
A. 5B. 6C. 7D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B 两乡分别由大米 200 吨、300 吨.现将这些大米运至 C、D 两个粮站储存.已知 C 粮站可 储存 240 吨,D 粮站可储存 200 吨,从 A 乡运往 C、D 两处的费用分别为每吨 20 元和 25 元,B 乡 运往 C、D 两处的费用分别为每吨 15 元和 18 元.设 A 乡运往 C 粮站大米 x 吨.A、B 两乡运往两 个粮站的运费分别为 yA、yB 元.
(1)请填写下表,并求出 yA、yB 与 x 的关系式:
C 站 | D 站 | 总计 | |
A 乡 | x 吨 | 200 吨 | |
B 乡 | 300 吨 | ||
总计 | 240 吨 | 260 吨 | 500 吨 |
(2)试讨论 A、B 乡中,哪一个的运费较少;
(3)若 B 乡比较困难,最多只能承受 4830 元费用,这种情况下,运输方案如何确定才能使总运费 最少?最少的费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,小明和父母一起开车到距家200千米的景点旅游.出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱剩余油量为30升.(假设行驶过程中汽车的耗油量是均匀的.)
(1)写出用行驶路程x(千米)来表示剩余油量Q(升)的代数式;
(2)当x=300千米时,求剩余油量Q的值;
(3)当油箱中剩余油量少于3升时,汽车将自动报警.如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若线段AB上有一点P,当PA=PB时,则称点P为线段AB的中点。
已知数轴上A,B两点对应数分别为a和b,![]() ,P为数轴上一动点,对应数为x.
,P为数轴上一动点,对应数为x.
(1)a=______,b=_______;
(2)若点P为线段AB的中点,则P点对应的数![]() 为______________.若B为线段AP的中点时则P点对应的数
为______________.若B为线段AP的中点时则P点对应的数![]() 为______________。
为______________。
(3)若点A、点B同时向左运动,它们的速度都为1个单位长度/秒,与此同时点P从-16处以2个单位长度/秒向右运动。
①设运动的时间为t秒,直接用含t的式子填空
AP=____________;BP=______________。
②经过多长时间后,点A、点B、点P三点中其中一点是另外两点的中点?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形组成的网格中,把一个点先沿水平方向平移丨a丨格(当a为正数时,表示向右平移;当a为负数时,表示向左平移),再沿竖直方向平移丨b|格(当b为正数时,表示向上平移;当b为负数时,表示向下平移),得到一个新的点,我们把这个过程记为(a,b)例如在图1中.从A到B记为:A→B(+1,+3)从c到D记为:C→D(+3,一3),请回答下列问题:
(1)如图1,若点A的运动路线为:A→B→D→A,请计算点A运动过的总路程;
(2)若点A运动的路线依次为:A→M(+2,+3)A→N(+1,―1),N→P
(-2,+2)P→Q(+4,—4)请你依次在图2上标出点M,N,P,Q的位置.
(3)在图2中,若点A经过(m,n)得到点E,点E再经过(p、,q)后得到Q,则m与p满足的数量关系是___________;n与q满足的数量关系是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:

(1)此次共调查了多少人?
(2)求文学社团在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有1500名学生,请估计喜欢体育类社团的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,抛物线与x轴交于A(﹣1,0),B(3,0),顶点为D(1,﹣4),点P为y轴上一动点.
(1)求抛物线的解析式;
(2)在y轴的负半轴上是否存在点P,使△BDP是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(3)如图2,点![]() 在抛物线上,求
在抛物线上,求![]() 的最小值.
的最小值.
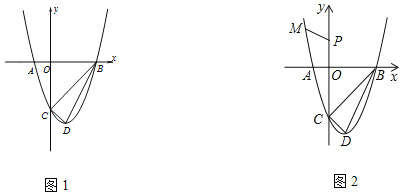
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M,N分别是射线AE,AF上的点,且PM=PN.

(1)如图1,当点M在线段AB上,点N在线段AC的延长线上时,求证:BM=CN;
(2)在(1)的条件下,直接写出线段AM,AN与AC之间的数量关系 ;
(3)如图2,当点M在线段AB的延长线上,点N在线段AC上时,若AC:PC=2:1,且PC=4,求四边形ANPM的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com