
【题目】在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.
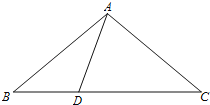
(1)若CD=CA=AB,请求出y与x的等量关系式;
(2)当D为边BC上一点,并且CD=CA,x=40,y=30时,则AB AC(填“=”或“≠”);
(3)如果把(2)中的条件“CD=CA”变为“CD=AB”,且x,y的取值不变,那么(1)中的结论是否仍成立?若成立请写出证明过程,若不成立请说明理由.
【答案】(1)3x+2y=180;(2)=;(3)成立.理由见解析
【解析】
试题分析:(1)由CD=CA,可表示出∠ADC的度数,又由三角形外角的性质,可得∠ADC=∠B+∠BAD,则可得方程:90﹣![]() x=x+y,继而求得答案;
x=x+y,继而求得答案;
(2)由CD=CA,x=40,y=30,首先可求得∠ADC的度数,继而证得CD=CA,则可求得∠C=∠B=40°,证得AB=AC;
(3)首先在BC上取点E,使BE=CD=AB,连接AE,易证得AD=AE,继而可得△ADB≌△AEC(SAS),则可证得结论.
解:(1)∵∠ABC=x°,CA=AB,
∴∠C=∠ABC=x°,
∵CD=CA,
∴∠ADC=∠CAD=![]() =90°﹣
=90°﹣![]() x°,
x°,
∵∠ADC=∠B+∠BAD,
∴90﹣![]() x=x+y,
x=x+y,
即:3x+2y=180;
(2)∵CD=CA,∠ABC=x°=40°,∠BAD=y°=30°,
∴∠ADC=∠ABC+∠BAD=70°,
∵CD=CA,
∴∠CAD=∠CDA=70°,
∴∠C=40°,
∴∠C=∠ABC,
∴AB=AC;
故答案为:=;
(3)成立.
理由:在BC上取点E,使BE=CD=AB,连接AE,
则∠AEB=∠EAB=![]() (180°﹣40°)=70°,
(180°﹣40°)=70°,
∴∠AEB=∠ADE=70°,
∴AD=AE,
∴∠ADB=∠AEC=180°﹣70°=110°,
∵BD=BE﹣DE,CE=CD﹣DE,
∴BD=EC,
在△ADB和△AEC中,
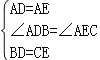 ,
,
∴△ADB≌△AEC(SAS),
∴AB=AC.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )
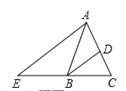
A. 40° B. 45° C. 60° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程x2 +(2m+1)x+m2-4=0.
的一元二次方程x2 +(2m+1)x+m2-4=0.
(1)若此方程有两个不相等的实数根,求m的取值范围.
(2)若方程的两个根分别是平行四边形的一组邻边的长,该平行四边形为菱形,求这个四边形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
中华优秀传统文化是中华民族的“根”和“魂”,是我们必须世代传承的文化根脉、文化基因.为传承优秀传统文化,某校为各班购进《三国演义》和《水浒传》连环画若干套,其中每套《三国演义》连环画的价格比每套《水浒传》连环画的价格贵60元,用4800元购买《水浒传》连环画的套数是用3600元购买《三国演义》连环画套数的2倍,求每套《水浒传》连环画的价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全民健身和医疗保健是社会普遍关注的问题.2014年,某社区共投入30万元用于购买健身器材和药品.2015年,该社区购买健身器材的费用比上一年增加50%,购买药品的费用比上一年减少![]() ,但社区在这两方面的总投入仍与2014年相同.
,但社区在这两方面的总投入仍与2014年相同.
(1)求2014年社区购买药品的总费用;
(2)据统计,2014年该社区积极健身的家庭达到200户,但其药品费用明显减少,只占当年购买药品总费用的![]() .与2014年相比,如果2015年社区内健身家庭户数增加的百分数与平均每户健身家庭的药品费用降低的百分数相同,那么,2015年该社区用于健身家庭的药品费用就是当年购买健身器材费用的
.与2014年相比,如果2015年社区内健身家庭户数增加的百分数与平均每户健身家庭的药品费用降低的百分数相同,那么,2015年该社区用于健身家庭的药品费用就是当年购买健身器材费用的![]() .求2015年该社区健身家庭的户数.
.求2015年该社区健身家庭的户数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】资料:小球沿直线撞击水平格档反弹时(不考虑垂直撞击),撞击路线与水平格档所成的锐角等于反弹路线与水平格档所成的锐角.以图(1)为例,如果黑球 ![]() 沿从
沿从 ![]() 到
到 ![]() 方向在
方向在 ![]() 点处撞击
点处撞击 ![]() 边后将沿从
边后将沿从 ![]() 到
到 ![]() 方向反弹,根据反弹原则可知
方向反弹,根据反弹原则可知 ![]() ,即
,即 ![]() .如图(2)和(3),
.如图(2)和(3),![]() 是一个长方形的弹子球台面,有黑白两球
是一个长方形的弹子球台面,有黑白两球 ![]() 和
和 ![]() ,小球沿直线撞击各边反弹时遵循资料中的反弹原则.(回答以下问题时将黑白两球均看作几何图形中的点,不考虑其半径大小)
,小球沿直线撞击各边反弹时遵循资料中的反弹原则.(回答以下问题时将黑白两球均看作几何图形中的点,不考虑其半径大小)

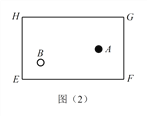
(1)探究(1):黑球 ![]() 沿直线撞击台边
沿直线撞击台边 ![]() 哪一点时,可以使黑球
哪一点时,可以使黑球 ![]() 经台边
经台边 ![]() 反弹一次后撞击到白球
反弹一次后撞击到白球 ![]() ?请在图(2)中画出黑球
?请在图(2)中画出黑球 ![]() 的路线图,标出撞击点,并简单证明所作路线是否符合反弹原则.
的路线图,标出撞击点,并简单证明所作路线是否符合反弹原则.
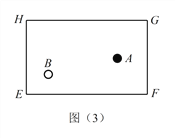
(2)探究(2):黑球 ![]() 沿直线撞击台边
沿直线撞击台边 ![]() 哪一点时,可以使黑球
哪一点时,可以使黑球 ![]() 先撞击台边
先撞击台边 ![]() 反弹一次后,再撞击台边
反弹一次后,再撞击台边 ![]() 反弹一次撞击到白球
反弹一次撞击到白球 ![]() ?请在图(3)中画出黑球
?请在图(3)中画出黑球 ![]() 的路线图,标出黑球撞击
的路线图,标出黑球撞击 ![]() 边的撞击点,简单说明作法,不用证明.
边的撞击点,简单说明作法,不用证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:
定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:(5+i)×(3-4i)=19-17i.
(1)填空:i3= ,i4= .
(2)计算:(3+i)2;
(3)试一试:请利用以前学习的有关知识将![]() 化简成a+bi的形式
化简成a+bi的形式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
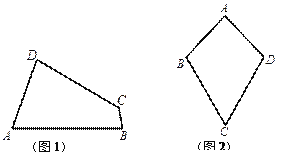
(1)已知:如图1,四边形![]() 是“等对角四边形”,
是“等对角四边形”, ![]() ,
, ![]() ,
, ![]() .求
.求![]() ,
, ![]() 的度数.
的度数.
(2)在探究“等对角四边形”性质时:
① 小红画了一个“等对角四边形”![]() (如图2),其中
(如图2),其中![]() ,
, ![]() ,此时她发现
,此时她发现![]() 成立.请你证明此结论.
成立.请你证明此结论.
② 由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形”![]() 中,
中, ![]() ,
, ![]() ,AB=AD=4,.求∠D和对角线
,AB=AD=4,.求∠D和对角线![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2004年4月我国铁路第5次大提速。假设Kl20次空调快速列车的平均速度提速后比提速前提高了44千米/时,提速前的列车时刻表如下:
行驶区间 | 车次 | 起始时刻 | 到站时刻 | 历时 | 全程里程 |
A地—B地 | K120 | 2:00 | 6:00 | 4小时 | 264千米 |
请你根据题目提供的信息,填写提速后的列车时刻表,并写出计算过程。
行驶区间 | 车次 | 起始时刻 | 到站时刻 | 历时 | 全程里程 |
A地—B地 | K120 | 2:00 | 264千米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com