
| k |
| x |
| k |
| x |
| 6 |
| x |
| 2+m+m |
| 2 |
| 3+0 |
| 2 |
| 3 |
| 2 |
| 6 |
| x |
| 3 |
| 2 |
| 3 |
| 2 |


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
A、“掷一枚硬币正面朝上的概率是
| ||
| B、一组数据2,2,3,6的众数和中位数都是2 | ||
| C、要了解全市人民的低碳生活状况,适宜采用抽样调查的方法 | ||
| D、随机抽取甲、乙两名同学的5次数学成绩,计算得平均分都是90分,方差分别是S2甲=5,S2乙=12,说明乙的成绩较为稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
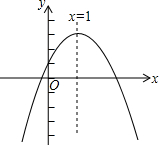 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com